题目内容
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|
考点:向量的加法及其几何意义
专题:等差数列与等比数列,平面向量及应用
分析:由题意,判定{an}是等差数列,求出公差d;{bn}是等比数列,求出公比q;求出向量
+
+
+…+
的坐标表示,计算即可.
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
解答:
解:在{an}中,a1=1,a5=13,an+2+an=2an+1,
∴{an}是等差数列,公差d=
(a5-a1)=3;
在{bn}中,b2=6,b3=3,bn+2bn=b
,
∴{bn}是等比数列,公比q=
=
;
∴向量
+
+
+…+
=(a2-a1,b2-b1)+(a4-a3,b4-b3)+(a6-a5,b6-b5)+…+(a2010-a2009,b2010-b2009)
=(1005d,-6-
-
-…-
)
=(3015,8[(
)2010-1]);
故选:C.
∴{an}是等差数列,公差d=
| 1 |
| 4 |
在{bn}中,b2=6,b3=3,bn+2bn=b
2 n+1 |
∴{bn}是等比数列,公比q=
| b3 |
| b2 |
| 1 |
| 2 |
∴向量
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
=(a2-a1,b2-b1)+(a4-a3,b4-b3)+(a6-a5,b6-b5)+…+(a2010-a2009,b2010-b2009)
=(1005d,-6-
| 6 |
| 41 |
| 6 |
| 42 |
| 6 |
| 41004 |
=(3015,8[(
| 1 |
| 2 |
故选:C.
点评:本题考查了等差、等比数列与平面向量的综合应用问题,是综合性题目.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥ax-2,则a的取值范围是( )
|
| A、[-2,2] | ||
| B、[-2,0] | ||
C、[1-2
| ||
D、[1-2
|
已知正数a,b满足:三数a,1,b的倒数成等差数列,则a+b的最小值为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
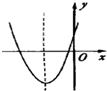 二次函数y=ax2+bx+c的图象如图所示,则a+b+c
二次函数y=ax2+bx+c的图象如图所示,则a+b+c 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=