题目内容
16．已知A={x|x2-x-6＜0}，B={x|2x≥1}，则A∩B=（ ）| A． | {x|1≤x＜3} | B． | {x|0≤x＜3} | C． | {x|1≤x＜2} | D． | {x|0＜x＜3} |
分析 先求出集合A和B，由此利用交集定义能求出A∩B．
解答 解：∵A={x|x2-x-6＜0}={x|-2＜x＜3}，
B={x|2x≥1}={x|x≥0}，
∴A∩B={x|0≤x＜3}．
故选：B．
点评 本题考查交集的解法，考查不等式的解法及应用，考查推理论证能力、运算求解能力，考查化归与转化思想，是基础题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
1．要得到y=sinx的图象只需将$y=sin（\frac{x}{2}+\frac{π}{3}）$的图象（ ）
| A． | 先向左平移$\frac{2π}{3}$单位，再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$ | |
| B． | 先向右平移$\frac{2π}{3}$单位，再将图象上各点的横坐标缩短至原来的$\frac{1}{2}$ | |
| C． | 先将图象上各点的横坐标缩短至原来的$\frac{1}{2}$，再将图象向左平移$\frac{π}{3}$单位 | |
| D． | 先将图象上各点横坐标扩大为原来的2倍，再将图象向右平移$\frac{π}{3}$单位 |
5．某几何体的三视图如图所示，则该几何体的外接球的体积为（ ）
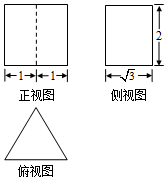
| A． | $\frac{4}{3}π$ | B． | $\frac{{32\sqrt{3}}}{27}π$ | C． | $\frac{{28\sqrt{3}}}{27}π$ | D． | $\frac{{28\sqrt{21}}}{27}π$ |
6．设等比数列{an}的前n项和为Sn，若$\frac{{S}_{6}}{{S}_{3}}$=7，则$\frac{{S}_{9}}{{S}_{6}}$=（ ）
| A． | 2 | B． | $\frac{7}{3}$ | C． | $\frac{13}{4}$ | D． | $\frac{43}{7}$ |