题目内容
5.某几何体的三视图如图所示,则该几何体的外接球的体积为( )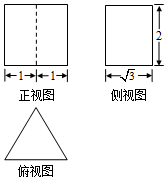
| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
分析 根据题意,由三视图分析可得,原几何体为三棱柱,同时可得其上下底面为边长以及高,设外接球的球心为O,半径为R,由三棱柱的几何结构分析可得R的值,代入球的体积公式计算可得答案.
解答  解:根据题意,由三视图分析可得,原几何体为三棱柱,
解:根据题意,由三视图分析可得,原几何体为三棱柱,
如图:其上下底面为边长为2的正三角形,其高为2,
设外接球的球心为O,半径为R,上下底面的中心为G′、G,
分析可得OG=1,AG=$\frac{2}{3}$×$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$,
则有R=OA=$\sqrt{1+\frac{4}{3}}$=$\sqrt{\frac{7}{3}}$,
其外接球体积V=$\frac{4π}{3}$($\sqrt{\frac{7}{3}}$)3=$\frac{28\sqrt{21}π}{27}$;
故选:D.
点评 本题考查几何体的三视图,涉及球的体积计算,关键是由三视图分析几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知A={x|x2-x-6<0},B={x|2x≥1},则A∩B=( )
| A. | {x|1≤x<3} | B. | {x|0≤x<3} | C. | {x|1≤x<2} | D. | {x|0<x<3} |
13.已知函数f(x)=2cosx-3sinx的导数为f'(x),则f'(x)=( )
| A. | f'(x)=-2sinx-3cosx | B. | f'(x)=-2cosx+3sinx | ||
| C. | f'(x)=-2sinx+3cosx | D. | f'(x)=2sinx-3cosx |