题目内容
7.已知函数$f(x)=tanx+\frac{1}{tanx}$,若f(α)=5,则f(-α)=-5.分析 判断f(x)的奇偶性.利用函数奇偶性得出答案.
解答 解:f(x)的定义域为{x|x≠$\frac{π}{2}$+kπ,k∈Z},关于原点对称,
f(-x)=tan(-x)+$\frac{1}{tan(-x)}$=-f(x),
∴f(x)是奇函数,
∴f(-α)=-f(α)=-5.
故答案为:-5.
点评 本题考查了函数奇偶性的性质,属于基础题.

练习册系列答案
相关题目
2.已知△ABC中,$a=\sqrt{2},b=\sqrt{3},A={45°}$,则三角形的解的个数( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个或1个 |
19.下列说法错误的是( )
| A. | 命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0” | |
| B. | “x>1”是“|x|>1”的充分不必要条件 | |
| C. | 若p且q为假命题,则p、q均为假命题 | |
| D. | 命题:“已知f(x)是R上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为“已知f(x)是R上的增函数,若f(a)+f(b)<f(-a)+f(-b),则a+b<0” |
16.已知A={x|x2-x-6<0},B={x|2x≥1},则A∩B=( )
| A. | {x|1≤x<3} | B. | {x|0≤x<3} | C. | {x|1≤x<2} | D. | {x|0<x<3} |
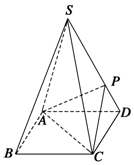 如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.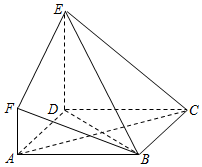 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°