题目内容
5．
如图，将全体正奇数排成一个三角形数阵，根据以上排列规律，数阵中第8行（从上向下数）第3个数（从左向右数）是95．
分析 斜着看，根据数阵的排列规律确定第10行（n≥3）从左向右的第3个数为第$\frac{10×9}{2}$+3=48个奇数即可．
解答 解：根据三角形数阵可知，斜着看，第n斜行奇数的个数为n个，则前n-1斜行奇数的总个数为1+2+3+…+（n-1）=$\frac{n（n-1）}{2}$，
则斜着看，第10行（n≥3）从左向右的第3个数为第$\frac{10×9}{2}$+3=48个奇数，
所以数阵中第8行（从上向下数）第3个数（从左向右数）是2×48-1=95．
故答案为95．
点评 本题主要考查归纳推理的应用，利用等差数列的通项公式是解决本题的关键．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
15．不等式3+5x-2x2＞0的解集为（ ）
| A． | （-3，$\frac{1}{2}$） | B． | （-∞，-3）∪（$\frac{1}{2}$，+∞） | C． | （-$\frac{1}{2}$，3） | D． | （-∞，-$\frac{1}{2}$）∪（3，+∞） |
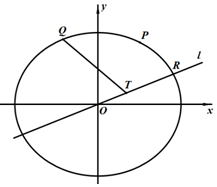如图，在平面直角坐标系xOy中，点$P（1，\frac{3}{2}）$和动点Q（m，n）都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）上，其中m＜0，n＞0．
14．若一圆弧长等于它所在圆的内接正三角形的边长，则该弧所对的圆心角弧度数为（ ）
| A． | $\frac{π}{3}$ | B． | $\sqrt{3}$ | C． | $\frac{2π}{3}$ | D． | 2 |