题目内容
10.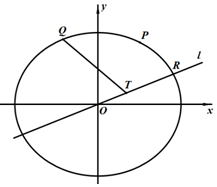 如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.
如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.(1)求椭圆的方程;
(2)若直线l的方程为3mx+4ny=0,点R(点R在第一象限)为直线l与椭圆的一个交点,点T在线段OR上,且QT=2.
①若m=-1,求点T的坐标;
②求证:直线QT过定点S,并求出定点S的坐标.
分析 (1)由离心率$e=\frac{c}{a}=\frac{1}{2}$,a=2c,$b=\sqrt{{a^2}-{c^2}}=\sqrt{3}c$,点$P(1,\frac{3}{2})$在椭圆上,代入即可求得c的值,即可求得椭圆方程;
(2)①设$T(t,-\frac{3m}{4n}t)$,由|QT|=2,由两点直线的距离公式可知:$(\frac{{9{m^2}}}{{16{n^2}}}+1){t^2}-\frac{1}{2}mt+{m^2}+{n^2}-4=0$,将Q点代入椭圆方程,${m^2}=4-\frac{{4{n^2}}}{3}$,代入$t=\frac{{4{n^2}}}{12-3m}$,由m=-1,即可求得T点坐标;②由①可知,$T(\frac{{4{n^2}}}{12-3m},-\frac{mn}{4-m})$,利用斜率公式可知:kQT=$\frac{n}{m-1}$,直线QT的方程为$y-n=\frac{n}{m-1}(x-m)$,即$y=\frac{n}{m-1}(x-1)$,
直线QT过定点(1,0).
解答 解:(1)由题意,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)焦点在x轴上,离心率$e=\frac{c}{a}=\frac{1}{2}$,
∴a=2c,$b=\sqrt{{a^2}-{c^2}}=\sqrt{3}c$,
∵点$P(1,\frac{3}{2})$在椭圆上,
∴$\frac{1^2}{{4{c^2}}}+\frac{{{{(\frac{3}{2})}^2}}}{{3{c^2}}}=1$,
解得:c=1,
∴$a=2,b=\sqrt{3}$,
∴椭圆C的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$; …(5分)
(2)①设$T(t,-\frac{3m}{4n}t)$,其中0<t<2,
∵|QT|=2,
∴$\sqrt{{{(m-t)}^2}+{{[n-(-\frac{3m}{4n}t)]}^2}}=2$,
即$(\frac{{9{m^2}}}{{16{n^2}}}+1){t^2}-\frac{1}{2}mt+{m^2}+{n^2}-4=0$,(*) …(7分)
∵点Q(m,n)在椭圆上,
∴$\frac{m^2}{4}+\frac{n^2}{3}=1$,则${m^2}=4-\frac{{4{n^2}}}{3}$,代入(*)式,
得$(\frac{{9+{n^2}}}{{4{n^2}}}){t^2}-\frac{1}{2}mt-\frac{1}{3}{n^2}=0$,$△={(-\frac{1}{2}m)^2}-4(\frac{{9+{n^2}}}{{4{n^2}}})(-\frac{1}{3}{n^2})=4$,
∴$t=\frac{{\frac{1}{2}m+2}}{{2×\frac{{9+{n^2}}}{{4{n^2}}}}}=\frac{{4{n^2}}}{12-3m}>0$或$t=\frac{{\frac{1}{2}m-2}}{{2×\frac{{9+{n^2}}}{{4{n^2}}}}}<0$,
∵0<t<2,
∴$t=\frac{{4{n^2}}}{12-3m}$,…(9分)
∴$T(\frac{{4{n^2}}}{12-3m},-\frac{mn}{4-m})$,
由题意,m=-1,
∴$\frac{{{{(-1)}^2}}}{4}+\frac{n^2}{3}=1$,
∵n>0,
∴$n=\frac{3}{2}$,
则T点坐标,$T(\frac{3}{5},\frac{3}{10})$…(11分)
②证明:由①可知,$T(\frac{{4{n^2}}}{12-3m},-\frac{mn}{4-m})$,
∴直线QT的斜率${k_{QT}}=\frac{{n-(-\frac{mn}{4-m})}}{{m-\frac{{4{n^2}}}{12-3m}}}=\frac{12n}{{12m-(3{m^2}+4{n^2})}}=\frac{12n}{12m-12}=\frac{n}{m-1}$,…(13分)
∴直线QT的方程为$y-n=\frac{n}{m-1}(x-m)$,
即$y=\frac{n}{m-1}(x-1)$,
∴直线QT过定点S(1,0). …(16分)
点评 本题考查椭圆的标准方程及简单几何性质,考查只有与椭圆的位置关系,直线的斜率公式,考查计算能力,属于中档题.

| A. | ±3 | B. | $±\;2\sqrt{2}$ | C. | ±2 | D. | ±1 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | (0,3) | B. | (1,3) | C. | (2,3) | D. | (-∞,-2)∪(0,+∞) |
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为$\sqrt{3}$;②AD是该圆的一条直径;③CD=$\frac{\sqrt{3}}{2}$;④四边形ABCD的面积S=$\frac{3\sqrt{3}}{4}$.其中正确结论的个数为( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为$\sqrt{3}$;②AD是该圆的一条直径;③CD=$\frac{\sqrt{3}}{2}$;④四边形ABCD的面积S=$\frac{3\sqrt{3}}{4}$.其中正确结论的个数为( ) 如图,将全体正奇数排成一个三角形数阵,根据以上排列规律,数阵中第8行(从上向下数)第3个数(从左向右数)是95.
如图,将全体正奇数排成一个三角形数阵,根据以上排列规律,数阵中第8行(从上向下数)第3个数(从左向右数)是95.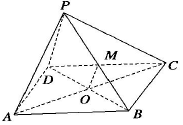 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )