题目内容
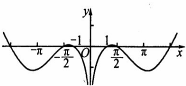
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
考点:函数的图象
专题:函数的性质及应用
分析:观察图象,从函数是否为奇函数还是偶函数,排除一些选项,再对自变量取特殊值,验证函数值是否与图象一致得出答案.
解答:
解:从图象上看函数的定义域为(-∞,0)∪(0,+∞),而B选项的函数的定义域为(0,+∞),排除B;
又函数的图象关于y轴对称,故函数为偶函数,
而选项D中的函数满足f(-x)=-f(x),所给的函数为奇函数,排除D;
选项A、C中的函数满足f(-x)=f(x),所给的函数为偶函数,只能在A、C中选,
从图象上看当x∈(0,1)时,f(x)<0,
A中,当x∈(0,1)时,sinx>0,所以
>0,故f(x)>0,排除A,
故选:C.
又函数的图象关于y轴对称,故函数为偶函数,
而选项D中的函数满足f(-x)=-f(x),所给的函数为奇函数,排除D;
选项A、C中的函数满足f(-x)=f(x),所给的函数为偶函数,只能在A、C中选,
从图象上看当x∈(0,1)时,f(x)<0,
A中,当x∈(0,1)时,sinx>0,所以
| sinx |
| x |
故选:C.
点评:本题主要考查函数的性质,如果借助函数的这些性质还不能够区分图象时,不妨考虑取特殊点(或局部范围)使问题求解得到突破

练习册系列答案
相关题目
设x,y满足约束条件
,则
的取值范围是( )
|
| x+y+2 |
| x+1 |
| A、[1,5] |
| B、[2,6] |
| C、[2,10] |
| D、[3,11] |
设实数列{an}和{bn}分别为等差数列与等比数列,且a1=b1=8,a4=b4=1,则以下结论正确的是( )
| A、a2>b2 |
| B、a3<b3 |
| C、a5>b5 |
| D、a6>b6 |
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )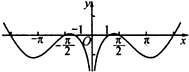

A、f(x)=
| ||
| B、f(x)=(lnx)cos2x | ||
| C、f(x)=(ln|x|)sin2x | ||
| D、f(x)=(ln|x|)cosx |