题目内容
在△ABC中,角A,B,C对边分别是a,b,c,满足2
•
=a2-(b+c)2.
(1)求角A的大小;
(2)求sinA•sinB•sinC的最大值,并求取得最大值时角B,C的大小.
| AB |
| AC |
(1)求角A的大小;
(2)求sinA•sinB•sinC的最大值,并求取得最大值时角B,C的大小.
考点:余弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)由2
•
=a2-(b+c)2.利用数量积运算可得:2bccosA=a2-(b+c)2,展开再利用余弦定理可得2bccosA=-2bccosA-2bc,化为cosA=-
.
(2)由A=
,可得C=
-B,0<B<
.利用两角和差的正弦公式、倍角公式可得sinA•sinB•sinC=
sinBsin(
-B)=
sin(2B+
)-
,由0<B<
.可得
<2B+
<
,当2B+
=
时,sinA•sinB•sinC取得最大值,即可得出.
| AB |
| AC |
| 1 |
| 2 |
(2)由A=
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| ||
| 4 |
| π |
| 6 |
| ||
| 8 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(1)∵
•
=cbcosA,2
•
=a2-(b+c)2.
∴2bccosA=a2-(b+c)2,展开为:2bccosA=a2-b2-c2-2bc,
∴2bccosA=-2bccosA-2bc,化为cosA=-
,
∵A∈(0,π).∴A=
.
(2)∵A=
,∴C=
-B,0<B<
.
∴sinA•sinB•sinC=
sinBsin(
-B)
=
sinB(
cosB-
sinB)
=
sinBcosB-
sin2B
=
sin2B-
(1-cos2B)
=
(
sin2B+
cos2B)-
=
sin(2B+
)-
,
∵0<B<
.∴
<2B+
<
,
当2B+
=
时,即B=
时,sinA•sinB•sinC取得最大值
,此时B=C=
.
| AB |
| AC |
| AB |
| AC |
∴2bccosA=a2-(b+c)2,展开为:2bccosA=a2-b2-c2-2bc,
∴2bccosA=-2bccosA-2bc,化为cosA=-
| 1 |
| 2 |
∵A∈(0,π).∴A=
| 2π |
| 3 |
(2)∵A=
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴sinA•sinB•sinC=
| ||
| 2 |
| π |
| 3 |
=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| 4 |
| ||
| 4 |
=
| 3 |
| 8 |
| ||
| 8 |
=
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 8 |
=
| ||
| 4 |
| π |
| 6 |
| ||
| 8 |
∵0<B<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
当2B+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| ||
| 8 |
| π |
| 6 |
点评:本题考查了数量积运算、余弦定理、两角和差的正弦公式、倍角公式、三角函数的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知随机变量ξ服从正态分布N(μ,δ2),且P(ξ<1)=0.5,P(ξ>2)=0.4,则P(0<ξ<1)=( )
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
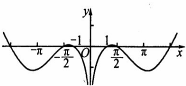

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
已知抛物线的焦点F(a,0)(a<0),则抛物线的标准方程是( )
| A、y2=4ax |
| B、y2=2ax |
| C、y2=-4ax |
| D、y2=-2ax |