题目内容
设x,y满足约束条件
,则
的取值范围是( )
|
| x+y+2 |
| x+1 |
| A、[1,5] |
| B、[2,6] |
| C、[2,10] |
| D、[3,11] |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
解答:
 解:设
解:设
=
=1+
,
设k=
,
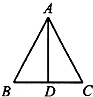
则k的几何意义是区域内的点与点D(-1,-1)的斜率,
作出不等式组对应的平面区域如图,其中A(0,4)
由图象知则DB的斜率最小,此时k=1,
DA的斜率最大,此时k=
=5,
即1≤k≤5,
则2≤1+k≤6,
故
的取值范围是[2,6],
故选:B.
 解:设
解:设| x+y+2 |
| x+1 |
| x+1+y+1 |
| x+1 |
| y+1 |
| x+1 |
设k=
| y+1 |
| x+1 |
则k的几何意义是区域内的点与点D(-1,-1)的斜率,
作出不等式组对应的平面区域如图,其中A(0,4)
由图象知则DB的斜率最小,此时k=1,
DA的斜率最大,此时k=
| 4+1 |
| 1 |
即1≤k≤5,
则2≤1+k≤6,
故
| x+y+2 |
| x+1 |
故选:B.
点评:本题主要考查线性规划的应用以及直线斜率的求解,利用数形结合是解决本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知随机变量ξ服从正态分布N(μ,δ2),且P(ξ<1)=0.5,P(ξ>2)=0.4,则P(0<ξ<1)=( )
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
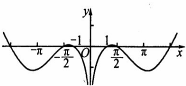

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |