题目内容
设M(x,y)到定点F(
,0)的距离和它到直线x=
距离的比是
.
(Ⅰ)求点M(x,y)的轨迹方程;
(Ⅱ)O为坐标原点,过F点且斜率为
的直线,与点M的轨迹交于点A(x1,y1),B(x2,y2),求△AOB的面积.
| 3 |
4
| ||
| 3 |
| ||
| 2 |
(Ⅰ)求点M(x,y)的轨迹方程;
(Ⅱ)O为坐标原点,过F点且斜率为
| ||
| 2 |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)直接利用已知条件考查方程,化简即可求点M(x,y)的轨迹方程;
(Ⅱ)设出直线AB的方程,与椭圆联立方程组消去y并整理利用韦达定理,结合x1x2+4y1y2=0,求出|AB|.原点O到直线AB的距离,然后求△AOB的面积.
(Ⅱ)设出直线AB的方程,与椭圆联立方程组消去y并整理利用韦达定理,结合x1x2+4y1y2=0,求出|AB|.原点O到直线AB的距离,然后求△AOB的面积.
解答:
解:(Ⅰ)由已知M(x,y)到定点F(
,0)的距离和它到直线x=
距离的比是
.
得
=
化简得点M(x,y)的轨迹方程为
+y2=1.…(6分)
(Ⅱ)设直线AB的方程为y=k(x-
).联立方程组
消去y并整理得(4k2+1)x2-8
k2x+12k2-4=0,
故x1+x2=
,x1x2=
,
y1y2=k(x1-
)•k(x2-
)=k2[x1x2-
(x1+x2)+3]=
又x1x2+4y1y2=0,所以
+
=0,
可得k2=
,所以x1+x2=
,x1x2=
由|AB|=
|x1-x2|=
×
=2
原点O到直线AB的距离d=
=
=1
所以S△AOB=
|AB|•d=1…(12分)
| 3 |
4
| ||
| 3 |
| ||
| 2 |
得
| ||||
|x-
|
| ||
| 2 |
化简得点M(x,y)的轨迹方程为
| x2 |
| 4 |
(Ⅱ)设直线AB的方程为y=k(x-
| 3 |
|
| 3 |
故x1+x2=
8
| ||
| 4k2+1 |
| 12k2-4 |
| 4k2+1 |
y1y2=k(x1-
| 3 |
| 3 |
| 3 |
| -k2 |
| 4k2+1 |
又x1x2+4y1y2=0,所以
| 12k2-4 |
| 4k2+1 |
| -4k2 |
| 4k2+1 |
可得k2=
| 1 |
| 2 |
4
| ||
| 3 |
| 2 |
| 3 |
由|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
原点O到直线AB的距离d=
|k(0-
| ||
|
|k
| ||
|
所以S△AOB=
| 1 |
| 2 |
点评:本题考查轨迹方程的求法,直线与椭圆方程的综合应用,考查分析问题解决问题的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
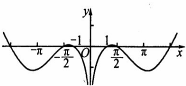

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
将函数y=cos(x+
)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移
个单位,所得函数图象的一个对称中心为( )
| π |
| 3 |
| π |
| 3 |
| A、(0,0) | ||
B、(
| ||
C、(
| ||
| D、(π,0) |
已知O是坐标原点,点A(-2,1),若点M(x,y)为平面区域
上的一个动点,则
•
的取值范围是( )
|
| OA |
| OM |
| A、[0,1] |
| B、[0,2] |
| C、[-1,0] |
| D、[-1,2] |
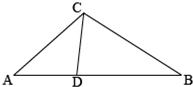 如图,在△ABC中,D为AB边上一点,DA=DC,已知B=
如图,在△ABC中,D为AB边上一点,DA=DC,已知B=