题目内容
设函数f(x)=cos(2x-
)-2
sinxcosx.
(Ⅰ)求f(x)的最小正周期,并指出由f(x)的图象如何变换得到函数y=cos2x的图象;
(Ⅱ)△ABC中角A,B,C的对边分别为a,b,c,若f(A-
)=
,b+c=2,求a的最小值.
| π |
| 3 |
| 3 |
(Ⅰ)求f(x)的最小正周期,并指出由f(x)的图象如何变换得到函数y=cos2x的图象;
(Ⅱ)△ABC中角A,B,C的对边分别为a,b,c,若f(A-
| π |
| 3 |
| 1 |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质,解三角形
分析:(I)由三角函数中的恒等变换应用化简函数解析式可得f(x)=cos(2x+
),根据周期公式即可求f(x)的最小正周期T.根据正弦函数的平移规律可得y=cos(2x+
)的图象向右平移
个单位长度得到函数y=cos2x.
(II)由已知及(I)可得cos(2A-
)=
,由A∈(0,π),可得A,由b+c=2及余弦定理,得a2=4-3bc,又bc≤(
)2=1即可求得a的最小值.
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
(II)由已知及(I)可得cos(2A-
| π |
| 3 |
| 1 |
| 2 |
| b+c |
| 2 |
解答:
解:(I)∵f(x)=
cos2x+
sin2x-
sin2x=
cos2x-
sin2x=cos(2x+
)(3分)
∴f(x)的最小正周期T=
=π,…(4分)
由y=cos(2x+
)的图象向右平移
个单位长度得到函数y=cos2x;…(6分)
(II)由f(A-
)=cos(2A-
)=
,A∈(0,π),可得A=
.…(8分)
由b+c=2及余弦定理,得a2=b2+c2-2bccos
=(b+c)2-3bc=4-3bc,…(10分)
又bc≤(
)2=1仅当b=c=1时bc取最大值,此时a取最小值1.…(12分)
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴f(x)的最小正周期T=
| 2π |
| 2 |
由y=cos(2x+
| π |
| 3 |
| π |
| 6 |
(II)由f(A-
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
由b+c=2及余弦定理,得a2=b2+c2-2bccos
| π |
| 3 |
又bc≤(
| b+c |
| 2 |
点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象,基本不等式的应用,属于基本知识的考查.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知随机变量ξ服从正态分布N(μ,δ2),且P(ξ<1)=0.5,P(ξ>2)=0.4,则P(0<ξ<1)=( )
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
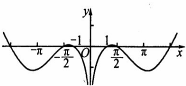

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
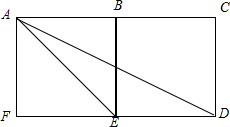 如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.
如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.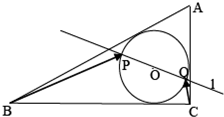 如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则
如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则