题目内容
已知函数f（x）的部分图象如图所示，则下列关于f（x）的表达式中正确的是（ ）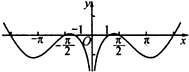
A、f（x）=
| ||
| B、f（x）=（lnx）cos2x | ||
| C、f（x）=（ln|x|）sin2x | ||
| D、f（x）=（ln|x|）cosx |
考点：函数的图象
专题：计算题,作图题,函数的性质及应用
分析：由图象可知函数f（x）为偶函数，从而判断函数的奇偶性即可．
解答：
解：由图象可知，函数f（x）为偶函数，
故f（x）=
为奇函数，故A不成立；
f（x）=（lnx）cos2x为非奇非偶函数，故B不成立；
f（x）=（ln|x|）sin2x为奇函数，故C不成立；
故选：D．
故f（x）=
| sinx |
| x2 |
f（x）=（lnx）cos2x为非奇非偶函数，故B不成立；
f（x）=（ln|x|）sin2x为奇函数，故C不成立；
故选：D．
点评：本题考查了函数的图象的应用及函数的性质的判断，属于基础题．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
已知函数f（x）的部分图象如图所示，则下列关于f（x）的表达式中正确的是（ ）
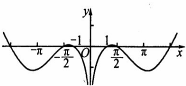
A、f（x）=
| ||
| B、f（x）=（lnx）tanx | ||
| C、f（x）=（ln|x|）cosx | ||
| D、f（x）=（ln|x|）sin2x |
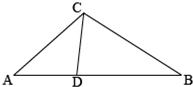如图，在△ABC中，D为AB边上一点，DA=DC，已知B=