题目内容
已知ABCD是矩形,A(6,5),B(5,6),E(-1,2)是CD边上一点.
(1)求矩形ABCD的面积;
(2)求矩形对角线AC所在直线的方程.
(1)求矩形ABCD的面积;
(2)求矩形对角线AC所在直线的方程.
考点:点到直线的距离公式,两点间距离公式的应用
专题:直线与圆
分析:(1)利用两点之间的距离可得|AB|,利用点斜式可得:直线AB的方程为:y-5=
(x-6),利用点到直线的距离公式可得:点E到直线AB的距离d.利用矩形ABCD的面积=|AB|×d即可得出.
(2)设C(x,y),则kAB•kBC=-1,kCE=kAB,解出C,再利用点斜式即可得出.
| 6-5 |
| 5-6 |
(2)设C(x,y),则kAB•kBC=-1,kCE=kAB,解出C,再利用点斜式即可得出.
解答:
解:(1)|AB|=
=
,
直线AB的方程为:y-5=
(x-6),化为x+y-11=0.
点E到直线AB的距离d=
=5
.
∴矩形ABCD的面积=|AB|×d=
×5
=10.
(2)设C(x,y),则kAB•kBC=-1,kCE=kAB,
∴-1×
=-1,
=-1,
解得x=0,y=1.∴C(0,1).
∴矩形对角线AC所在直线的方程为y=
x+1,化为2x-3y+3=0.
| 12+12 |
| 2 |
直线AB的方程为:y-5=
| 6-5 |
| 5-6 |
点E到直线AB的距离d=
| |-1+2-11| | ||
|
| 2 |
∴矩形ABCD的面积=|AB|×d=
| 2 |
| 2 |
(2)设C(x,y),则kAB•kBC=-1,kCE=kAB,
∴-1×
| y-6 |
| x-5 |
| y-2 |
| x+1 |
解得x=0,y=1.∴C(0,1).
∴矩形对角线AC所在直线的方程为y=
| 5-1 |
| 6-0 |
点评:本题考查了相互平行、垂直的直线斜率之间的关系、点斜式、两点之间的距离关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
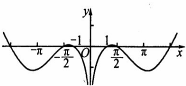

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
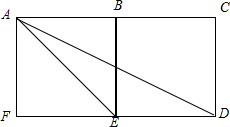 如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.
如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.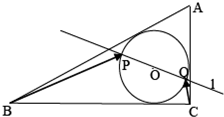 如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则
如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则