题目内容
设实数列{an}和{bn}分别为等差数列与等比数列,且a1=b1=8,a4=b4=1,则以下结论正确的是( )
| A、a2>b2 |
| B、a3<b3 |
| C、a5>b5 |
| D、a6>b6 |
考点:等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:由题意可得数列的公差和公比,进而可得选项中的各个值,比较可得.
解答:
解:∵a1=8,a4=1,∴d=
=-
,
∵b1=8,b4=1,∴q3=
=
,∴q=
,
∴b2=4<a2=
,∴b3=2<a3=
,
∴b5=
>a5=-
,∴b6=
>a6=-
,
故选:A
| a4-a1 |
| 4-1 |
| 7 |
| 3 |
∵b1=8,b4=1,∴q3=
| b4 |
| b1 |
| 1 |
| 8 |
| 1 |
| 2 |
∴b2=4<a2=
| 17 |
| 3 |
| 10 |
| 3 |
∴b5=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 4 |
| 11 |
| 3 |
故选:A
点评:本题考查等差数列和等比数列的通项公式,属基础题.

练习册系列答案
相关题目
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
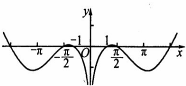

A、f(x)=
| ||
| B、f(x)=(lnx)tanx | ||
| C、f(x)=(ln|x|)cosx | ||
| D、f(x)=(ln|x|)sin2x |
已知O是坐标原点,点A(-2,1),若点M(x,y)为平面区域
上的一个动点,则
•
的取值范围是( )
|
| OA |
| OM |
| A、[0,1] |
| B、[0,2] |
| C、[-1,0] |
| D、[-1,2] |