题目内容
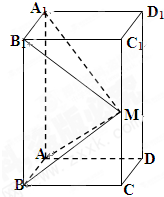 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点(1)求异面直线A1M与C1D1所成的角的正切值;
(2)求证:平面ABM⊥平面A1B1M;
(3)求三棱锥B-A1B1M的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离,空间角
分析:(1)取DD1中点N,连接MN,NA1.证明∠A1MN是异面直线A1M与C1D1所成的角或其补角,
(2)由题设条件,先证明BM⊥平面A1B1M,再由BM?平面ABM,证明出平面ABM⊥平面A1B1M.
(3)利用V=
•S△ABM•BM可求三棱锥B-A1B1M的体积.
(2)由题设条件,先证明BM⊥平面A1B1M,再由BM?平面ABM,证明出平面ABM⊥平面A1B1M.
(3)利用V=
| 1 |
| 3 |
解答:
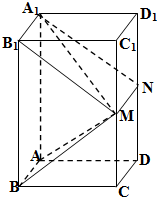 (1)证明:取DD1中点N,连接MN,NA1.
(1)证明:取DD1中点N,连接MN,NA1.
因为C1M∥D1N,且C1M=D1N,所以MN∥C1D1.
所以∠A1MN是异面直线A1M与C1D1所成的角或其补角,
MN=C1D1=1,A1N=
,A1M=
,
因为MN2+A1N2=A1M2,所以∠A1NM=90°,
所以tan∠A1MN=
=
=
. …(4分)
(2)证明:由A1B1⊥平面BCC1B1,BM?平面BCC1B1,得A1B1⊥BM,①
∵A1B1⊥平面BCC1B,∴∠A1B1M=90°,
而A1B1=1,B1M=
,
又BM=
,B1B=2,
∴B1M2+BM2=B1B2,从而BM⊥B1M
又A1B1∩B1M=B1,再由①,②得BM⊥平面A1B1M,
而BM?平面ABM,
∴平面ABM⊥平面A1B1M.
(3)设三棱锥B-A1B1M的体积为V,则V=
•S△ABM•BM=
×
×1×
×
=
.
 (1)证明:取DD1中点N,连接MN,NA1.
(1)证明:取DD1中点N,连接MN,NA1.因为C1M∥D1N,且C1M=D1N,所以MN∥C1D1.
所以∠A1MN是异面直线A1M与C1D1所成的角或其补角,
MN=C1D1=1,A1N=
| 2 |
| 3 |
因为MN2+A1N2=A1M2,所以∠A1NM=90°,
所以tan∠A1MN=
| A1N |
| MN |
| ||
| 1 |
| 2 |
(2)证明:由A1B1⊥平面BCC1B1,BM?平面BCC1B1,得A1B1⊥BM,①
∵A1B1⊥平面BCC1B,∴∠A1B1M=90°,
而A1B1=1,B1M=
| 2 |
又BM=
| 2 |
∴B1M2+BM2=B1B2,从而BM⊥B1M
又A1B1∩B1M=B1,再由①,②得BM⊥平面A1B1M,
而BM?平面ABM,
∴平面ABM⊥平面A1B1M.
(3)设三棱锥B-A1B1M的体积为V,则V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成的角的求法,考查三棱锥B-A1B1M的体积,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知函数f(x)=
x2+4lnx,若存在满足1≤x0≤3的实数x0,使得曲线f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
| 1 |
| 2 |
| A、[5,+∞) | ||
| B、[4,5] | ||
C、[4,
| ||
| D、(-∞,4] |