题目内容
已知函数f(x)=
的图象关于y=x对称,则a=( )
| ax-1 |
| x+2 |
| A、-4 | B、-2 | C、2 | D、4 |
考点:反函数
专题:函数的性质及应用
分析:由于函数f(x)=
的图象关于y=x对称,可得函数f(x)=
的反函数是它本身,求出其反函数并进行比较即可得出.
| ax-1 |
| x+2 |
| ax-1 |
| x+2 |
解答:
解:∵函数f(x)=
的图象关于y=x对称,∴函数f(x)=
的反函数是它本身.
由y=
(x≠2),解得x=
(y≠a),把x与y互换可得y=
=
,
由于y=
与y=
是同一个函数,∴a=-2.
故选:B.
| ax-1 |
| x+2 |
| ax-1 |
| x+2 |
由y=
| ax-1 |
| x+2 |
| 2y+1 |
| a-y |
| 2x+1 |
| a-x |
| -2x-1 |
| x-a |
由于y=
| -2x-1 |
| x-a |
| ax-1 |
| x+2 |
故选:B.
点评:本题考查了求反函数的方法及其性质,属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知椭圆两焦点坐标分别是F1(-2,0),F2(2,0),并且经过点M(-
,
),则椭圆的标准方程为( )
| 5 |
| 2 |
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}满足a2+a12+2a5=120,则a6为( )
| A、40 | B、36 | C、30 | D、15 |
已知a∈[-1,1],则x2+(a-4)x+4-2a>0的解为( )
| A、x>3或x<2 |
| B、x>2或x<1 |
| C、x>3或x<1 |
| D、1<x<3 |
cos(
-a)等于( )
| 3π |
| 2 |
| A、sina | B、cosa |
| C、-sina | D、-cosa |
已知等差数列{an}中,a1+a2+a3=5,a7+a8+a9=10,则a4+a5+a6=( )
A、5
| ||
| B、15 | ||
C、
| ||
| D、50 |
已知x<y<0,则有( )
| A、0<x2<xy |
| B、y2<xy<x2 |
| C、xy<y2<x2 |
| D、y2>x2>0 |
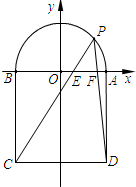 如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.
如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.