题目内容
已知x，y∈R+，且x+y=3，则
+
的最小值为（ ）
| 1 |
| x |
| 1 |
| y |
| A、4 | ||
B、
| ||
C、
| ||
D、
|
考点：基本不等式
专题：不等式的解法及应用
分析：利用“乘1法”和基本不等式即可得出．
解答：
解：∵x，y∈R+，且x+y=3，
∴
+
=
(x+y)(
+
)≥
(2+
+
)≥
(2+2
)=
，当且仅当x=y=
时取等号．
因此
+
的最小值为
．
故选：B．
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| 3 |
| y |
| x |
| x |
| y |
| 1 |
| 3 |
|
| 4 |
| 3 |
| 3 |
| 2 |
因此
| 1 |
| x |
| 1 |
| y |
| 4 |
| 3 |
故选：B．
点评：本题考查了“乘1法”和基本不等式，属于基础题．
练习册系列答案
相关题目
函数y=sinx，y=cosx和y=tanx具有相同单调性的一个区间是（ ）
A、（0，
| ||
B、（
| ||
C、（π，
| ||
D、（-
|
已知a∈[-1，1]，则x2+（a-4）x+4-2a＞0的解为（ ）
| A、x＞3或x＜2 |
| B、x＞2或x＜1 |
| C、x＞3或x＜1 |
| D、1＜x＜3 |
已知等差数列{an}中，a1+a2+a3=5，a7+a8+a9=10，则a4+a5+a6=（ ）
A、5
| ||
| B、15 | ||
C、
| ||
| D、50 |
已知x＜y＜0，则有（ ）
| A、0＜x2＜xy |
| B、y2＜xy＜x2 |
| C、xy＜y2＜x2 |
| D、y2＞x2＞0 |
已知f（x）是定义在R上的偶函数，且在（-∞，0]是减函数，设a=f（log26），b=f(log
3)，c=f(
)则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、c＜b＜a |
| B、b＜c＜a |
| C、b＜a＜c |
| D、a＜b＜c |
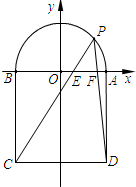如图，点P是半圆C：x2+y2=1（y≥0）上位于x轴上方的任意一点，A、B是直径的两个端点，以AB为一边作正方形ABCD，PC交AB于E，PD交AB于F，求证：BE，EF，FA成等比数列．