题目内容
已知函数y=xlnx，求其在点x=1处的切线方程．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求导函数，确定切线的斜率，切点的坐标，利用点斜式可得切线方程．
解答：
解：∵y=xlnx，
∴y′=1×lnx+x•
=1+lnx，
∴x=1时，y′=1．
又当x=1时，y=0，
∴在点x=1处的切线方程为y=x-1．
∴y′=1×lnx+x•
| 1 |
| x |
∴x=1时，y′=1．
又当x=1时，y=0，
∴在点x=1处的切线方程为y=x-1．
点评：本题考查导数的几何意义，考查导数知识的运用，考查学生的计算能力，属于基础题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
已知a∈[-1，1]，则x2+（a-4）x+4-2a＞0的解为（ ）
| A、x＞3或x＜2 |
| B、x＞2或x＜1 |
| C、x＞3或x＜1 |
| D、1＜x＜3 |
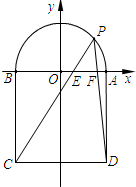如图，点P是半圆C：x2+y2=1（y≥0）上位于x轴上方的任意一点，A、B是直径的两个端点，以AB为一边作正方形ABCD，PC交AB于E，PD交AB于F，求证：BE，EF，FA成等比数列．