题目内容
过原点的二次函数y=f(x)的顶点为(-1,-1)
(1)求y=f(x)的解析式;
(2)求h(x)=f(lgx),(x>0)的单调区间;
(3)若g(x)=
,x∈R的值域为[
,2],求实数k的值.
(1)求y=f(x)的解析式;
(2)求h(x)=f(lgx),(x>0)的单调区间;
(3)若g(x)=
| f(x)+k |
| x2+x+1 |
| 2 |
| 3 |
考点:复合函数的单调性,函数的值域,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)设出二次函数的顶点式,由函数图象经过原点求得二次项系数,则函数解析式可求;
(2)由符合函数的单调性求解函数的单调区间;
(3)利用判别式法求解函数g(x)的值域,得到关于y的不等式后,不等式对应二次方程的根是值域端点值,然后利用根与系数关系求解k的值.
(2)由符合函数的单调性求解函数的单调区间;
(3)利用判别式法求解函数g(x)的值域,得到关于y的不等式后,不等式对应二次方程的根是值域端点值,然后利用根与系数关系求解k的值.
解答:
解:(1)∵二次函数y=f(x)的顶点为(-1,-1),
∴设二次函数f(x)=a(x+1)2-1,
又二次函数经过原点,则0=a(0+1)2-1,解得a=1.
∴y=f(x)的解析式为f(x)=(x+1)2-1=x2+2x;
(2)h(x)=f(lgx),
外层函数y=f(x)在(-∞,-1)上为减函数,在[-1,+∞)上为增函数,
由lgx=-1,得:x=
.
而内层函数y=lgx在(0,+∞)上为增函数,
由复合函数的单调性知:当x∈(0,
)时,函数h(x)=f(lgx)为减函数,
当x∈[
,+∞)时,函数h(x)=f(lgx)为增函数;
(3)令y=g(x)=
=
,得
(y-1)x2+(y-2)x+y-k=0.
由△=(y-2)2-4(y-1)(y-k)=-3y2+4ky+4-4k≥0,得
3y2-4ky-4+4k≤0.
∵g(x)=
,x∈R的值域为[
,2],
则
+2=
,解得k=2.
∴设二次函数f(x)=a(x+1)2-1,
又二次函数经过原点,则0=a(0+1)2-1,解得a=1.
∴y=f(x)的解析式为f(x)=(x+1)2-1=x2+2x;
(2)h(x)=f(lgx),
外层函数y=f(x)在(-∞,-1)上为减函数,在[-1,+∞)上为增函数,
由lgx=-1,得:x=
| 1 |
| 10 |
而内层函数y=lgx在(0,+∞)上为增函数,
由复合函数的单调性知:当x∈(0,
| 1 |
| 10 |
当x∈[
| 1 |
| 10 |
(3)令y=g(x)=
| f(x)+k |
| x2+x+1 |
| x2+2x+k |
| x2+x+1 |
(y-1)x2+(y-2)x+y-k=0.
由△=(y-2)2-4(y-1)(y-k)=-3y2+4ky+4-4k≥0,得
3y2-4ky-4+4k≤0.
∵g(x)=
| f(x)+k |
| x2+x+1 |
| 2 |
| 3 |
则
| 2 |
| 3 |
| 4k |
| 3 |
点评:本题考查了函数解析式的求解及常用方法,训练了复合函数的单调性的求法,考查了利用判别式法求函数的值域,体现了数学转化思想方法,是有一定难度题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
+(x-1)0的定义域为( )
| 1 | ||
|
A、(-
| ||
| B、(-2,1)∪(1,+∞) | ||
C、(-
| ||
| D、(0,1)∪(1,+∞) |
已知等差数列{an}中,a1+a2+a3=5,a7+a8+a9=10,则a4+a5+a6=( )
A、5
| ||
| B、15 | ||
C、
| ||
| D、50 |
已知f(x)是定义在R上的偶函数,且在(-∞,0]是减函数,设a=f(log26),b=f(log
3),c=f(
)则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<b<c |
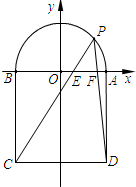 如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.
如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.