题目内容
已知三条直线a，b，c，若a和b是异面直线，b和c是异面直线，那么直线a和c的位置关系是（ ）
| A、平行 | B、相交 |
| C、异面 | D、平行、相交或异面 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：作出一个正方体，借助正方体的空间结构能够求出结果．
解答：
解：
在正方体ABCD-A1B1C1D1中，
取D1C1=a，BB1=b，
若取DC=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是平行直线；
若取A1D1=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是相交直线；
若取AD=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是异面直线．
综上：直线a和c的位置关系是平行、相交或异面．
故选：D．
在正方体ABCD-A1B1C1D1中，取D1C1=a，BB1=b，
若取DC=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是平行直线；
若取A1D1=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是相交直线；
若取AD=c时，
则a和b是异面直线，b和c是异面直线，直线a和c是异面直线．
综上：直线a和c的位置关系是平行、相交或异面．
故选：D．
点评：本题考查空间直线的位置关系，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
到两坐标轴的距离之和为6的点的轨迹方程是（ ）
| A、x+y=6 |
| B、x±y=6 |
| C、|x|+|y|=6 |
| D、|x+y|=6 |
已知椭圆两焦点坐标分别是F1（-2，0），F2（2，0），并且经过点M(-
，
)，则椭圆的标准方程为（ ）
| 5 |
| 2 |
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=sinx，y=cosx和y=tanx具有相同单调性的一个区间是（ ）
A、（0，
| ||
B、（
| ||
C、（π，
| ||
D、（-
|
已知三棱锥A-BCD中，平面ABD⊥平面BCD，BC⊥CD，BC=CD=4，AB=AD=2
，则三棱锥A-BCD的外接球的大圆面积为（ ）
| 3 |
| A、36π | B、27π |
| C、12π | D、9π |
函数f(x)=
+(x-1)0的定义域为（ ）
| 1 | ||
|
A、(-
| ||
| B、（-2，1）∪（1，+∞） | ||
C、(-
| ||
| D、（0，1）∪（1，+∞） |
已知等差数列{an}满足a2+a12+2a5=120，则a6为（ ）
| A、40 | B、36 | C、30 | D、15 |
已知a∈[-1，1]，则x2+（a-4）x+4-2a＞0的解为（ ）
| A、x＞3或x＜2 |
| B、x＞2或x＜1 |
| C、x＞3或x＜1 |
| D、1＜x＜3 |
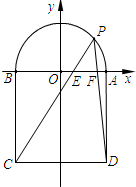如图，点P是半圆C：x2+y2=1（y≥0）上位于x轴上方的任意一点，A、B是直径的两个端点，以AB为一边作正方形ABCD，PC交AB于E，PD交AB于F，求证：BE，EF，FA成等比数列．