题目内容
3.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}}\right.$目标函数z=2log4y-log2x,则z的最大值为1.分析 先画出满足不等式组$\left\{{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}}\right.$的平面区域,然后分析z=2log4y-log2x的几何意义,进而给出z的取值范围.
解答  解:实数x,y满足不等式组$\left\{{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}}\right.$平面区域,如下图所示:
解:实数x,y满足不等式组$\left\{{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}}\right.$平面区域,如下图所示:
∵目标函数z=2log4y-log2x=log2$\frac{y}{x}$,其中$\frac{y}{x}$表示区域内点P与O(0,0)点连线的斜率,由$\left\{\begin{array}{l}{y=2}\\{x+2y-5=0}\end{array}\right.$,解得A(1,2)
又∵当点P在A时,即当x=1,y=2时,$\frac{y}{x}$取得最大值,z最大,最大值为z=1,
故答案为:1.
点评 平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
18.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
15.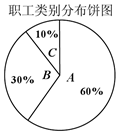 某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
对于A、B、C三类工种职工每人每年保费分别为a元,a元,b元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费a、b所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业与保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择方案2的支出(不包括职工支出)低于选择方案1的支出期望,求保费a、b所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
 某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费a、b所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业与保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择方案2的支出(不包括职工支出)低于选择方案1的支出期望,求保费a、b所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
12.某印刷厂为了研究印刷单册书籍的成本y(单位:元)与印刷册数x(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:${\hat y^{(1)}}=\frac{4}{x}+1.1$,方程乙:${\hat y^{(2)}}=\frac{6.4}{x^2}+1.6$.
(I)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
②分别计算模型甲与模型乙的残差平方和Q1及Q2,并比较Q1,Q2的大小,判断哪个模型拟合效果更好.
(II)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.7)或16千册(概率0.3),若印刷厂以每册5元的价格将书籍出售给订货商,估计印刷厂二次印刷8千册还是16千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
(I)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\hat y_i}^{(1)}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\hat e_i}^{(1)}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值${\hat y_i}^{(2)}$ | 2.3 | 2 | 1.9 | ||
| 残差${\hat e_i}^{(2)}$ | 0.1 | 0 | 0 | |||
(II)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.7)或16千册(概率0.3),若印刷厂以每册5元的价格将书籍出售给订货商,估计印刷厂二次印刷8千册还是16千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
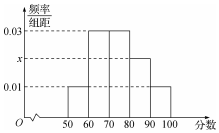 2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).