Question

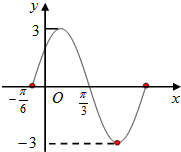如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的部分图象，
（1）求函数f（x）的解析式；
（2）当x∈(-

π

2

，0)时，求函数的值域．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：综合题,三角函数的图像与性质

分析：（1）由图知A=3，T=π，从而可知ω=2，由曲线过（-

π

6

，0））可求得φ，从而可得函数表达式；
（2）利用正弦函数的值域，可求x∈(-

π

2

，0)时，求函数的值域．

解答： 解：（1）由图可知：A=3，

T

2

=

π

3

-（-

π

6

）=

π

2

，即T=π，
∴ω=2，
∴f（x）=3sin（2x+φ）…（2分）
又由图可知：（-

π

6

，0）是五点作图法中的第一点，
∴2×（-

π

6

）+φ=0，即φ=

π

3

，…（4分）
∴f（x）=3sin（2x+

π

3

）．…（5分）
（2）∵x∈(-

π

2

，0)，
∴-

2π

3

＜2x+

π

3

＜

π

3

，…（7分）
∴-1≤sin（2x+

π

3

）＜

3

2

，即-3≤3sin（2x+

π

3

）＜

3 3

2

．…（9分）
∴函数f（x）在x∈(-

π

2

，0)上的值域是[-3，

3 3

2

）．…（10分）

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查识图与运算求解能力，属于中档题．