题目内容
集合A={y|y=x3,x∈[1,2]},集合B={x|lnx-ax+2>0},且A⊆B,则实数a的取值范围是 .
考点:集合的包含关系判断及应用
专题:计算题
分析:先求出集合A,将A⊆B转化为lnx-ax+2>0在[1,8],上恒成立,构造函数y=
,x∈[1,8],利用导数求出当x=8时有最小值为
=
,得到参数a的范围.
| lnx+2 |
| x |
| 2+ln8 |
| 8 |
| 2+3ln2 |
| 8 |
解答:
解:A={y|y=x3,x∈[1,2]}={y|1≤y≤8},
∵A⊆B,
∴lnx-ax+2>0在[1,8]上恒成立,
∴a<
在[1,8]上恒成立,
令y=
,x∈[1,8],
下面求y=
,x∈[1,8]的最小值,
∵y′=
<0,
∴当x∈[1,8]时,y=
单调递减,
∴当x=8时有最小值为
=
,
∴a的范围为a<
,
故答案为:(-∞,
).
∵A⊆B,
∴lnx-ax+2>0在[1,8]上恒成立,
∴a<
| lnx+2 |
| x |
令y=
| lnx+2 |
| x |
下面求y=
| lnx+2 |
| x |
∵y′=
| -lnx-1 |
| x2 |
∴当x∈[1,8]时,y=
| lnx+2 |
| x |
∴当x=8时有最小值为
| 2+ln8 |
| 8 |
| 2+3ln2 |
| 8 |
∴a的范围为a<
| 2+3ln2 |
| 8 |
故答案为:(-∞,
| 2+3ln2 |
| 8 |
点评:本题考查的是集合的包含关系,函数的值域,不等式恒成立,分离参数求最值,是一道中档题.

练习册系列答案
相关题目
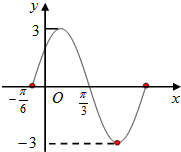 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|