题目内容
已知函数f(x)=lnx+
-
(a∈R)
(1)当a=2时,求函数f(x)在点P(1,f(1))处的切线方程;
(2)若函数f(x)在(0,+∞)上为增函数,求a的取值范围;
(3)设x1>x2>0,求证
<x1+x2.
| a |
| x+1 |
| a |
| 2 |
(1)当a=2时,求函数f(x)在点P(1,f(1))处的切线方程;
(2)若函数f(x)在(0,+∞)上为增函数,求a的取值范围;
(3)设x1>x2>0,求证
| x1-x2 |
| lnx1-lnx2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)把a=1代入函数解析式,求出导函数得到f′(1),再求出f(1)的值,利用直线方程的点斜式得切线方程;
(2)由原函数的导函数在(0,+∞)上大于等于0恒成立得到a≤x+
+2对x∈(0,+∞)上恒成立,然后利用基本不等式求得不等式右边的最小值,则a的范围可求;
(3)利用分析法把要证明的不等式转化为证明
-1<(
+1)ln
,令
=t (t>1)换元后引入辅助函数h(t)=(t+1)lnt-t+1(t>1),然后利用导数证明.
(2)由原函数的导函数在(0,+∞)上大于等于0恒成立得到a≤x+
| 1 |
| x |
(3)利用分析法把要证明的不等式转化为证明
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
解答:
(1)解:当a=2时,f(x)=lnx+
-1,
f′(x)=
-
(x>0),
∴k=f′(1)=
.
由f(1)=0,
∴求函数f(x)在点P(1,f(1))处的切线方程为x-2y-1=0;
(2)解:∵f(x)=lnx+
-
,
∴f′(x)=
-
=
(x>0).
由题意得(x+1)2-ax≥0对x∈(0,+∞)上恒成立,
∴a≤x+
+2对x∈(0,+∞)上恒成立,
∴a≤(x+
+2)min,
∵x+
+2≥2
+2=4 (当且仅当x=1时取等号),
∴a≤4;
(3)证明:∵x1>x2>0,
∴lnx1-lnx2>0.
要证
<x1+x2,
只要证x1-x2<(x1+x2)(lnx1-lnx2),
即证x1-x2<(x1+x2)ln
,
也就是证
-1<(
+1)ln
.
令
=t (t>1),不等式化为t-1<(t+1)lnt (t>1),
令h(t)=(t+1)lnt-t+1(t>1).
只要证h(t)=(t+1)lnt-t+1>0成立,
由(1)知当a=2时,h(t)=f(t)(t+1),
只要证f(t)=lnt+
-1>0成立,
当a=2时,由(2)可知函数f(t)在(1,+∞)上单调递增,
∴f(t)>f(1)=0,
∴x1>x2>0时,
<x1+x2成立.
| 2 |
| x+1 |
f′(x)=
| 1 |
| x |
| 2 |
| (x+1)2 |
∴k=f′(1)=
| 1 |
| 2 |
由f(1)=0,
∴求函数f(x)在点P(1,f(1))处的切线方程为x-2y-1=0;
(2)解:∵f(x)=lnx+
| a |
| x+1 |
| a |
| 2 |
∴f′(x)=
| 1 |
| x |
| a |
| (x+1)2 |
| (x+1)2-ax |
| x(x+1)2 |
由题意得(x+1)2-ax≥0对x∈(0,+∞)上恒成立,
∴a≤x+
| 1 |
| x |
∴a≤(x+
| 1 |
| x |
∵x+
| 1 |
| x |
x•
|
∴a≤4;
(3)证明:∵x1>x2>0,
∴lnx1-lnx2>0.
要证
| x1-x2 |
| lnx1-lnx2 |
只要证x1-x2<(x1+x2)(lnx1-lnx2),
即证x1-x2<(x1+x2)ln
| x1 |
| x2 |
也就是证
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
令
| x1 |
| x2 |
令h(t)=(t+1)lnt-t+1(t>1).
只要证h(t)=(t+1)lnt-t+1>0成立,
由(1)知当a=2时,h(t)=f(t)(t+1),
只要证f(t)=lnt+
| 2 |
| t+1 |
当a=2时,由(2)可知函数f(t)在(1,+∞)上单调递增,
∴f(t)>f(1)=0,
∴x1>x2>0时,
| x1-x2 |
| lnx1-lnx2 |
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的单调性.训练了利用换元法和构造函数法证明不等式,是压轴题.

练习册系列答案
相关题目
集合A={α|α=
,n∈Z}∪{α|α=2nπ±
π,n∈Z},B={β|β=
,n∈Z}∪{β|β=nπ+
π,n∈Z},则A、B之间关系为( )
| nπ |
| 2 |
| 2 |
| 3 |
| 2nπ |
| 3 |
| 1 |
| 2 |
| A、B?A | B、A?B |
| C、B?A | D、A?B |
 如图,在正四棱锥P-ABCD中,PA=AB=
如图,在正四棱锥P-ABCD中,PA=AB=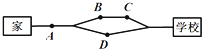 小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是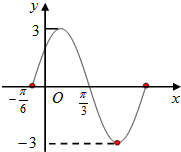 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|