已知实数x.y满足y≤x-1x≤3x+5y≥4.则x2y的最小值是．题目和参考答案——青夏教育精英家教网—

题目内容

已知实数x，y满足

y≤x-1

x≤3

x+5y≥4

，则

的最小值是

．

考点：简单线性规划

专题：不等式的解法及应用

分析：设z=

，则x²=zy，作出不等式组对应的平面区域，利用数形结合即可得到结论．

解答： 解：作出不等式组对应的平面区域如图：

由图象可知x＞0，y＞0
设z=

，则x²=zy，（z＞0），对应的曲线为抛物线，
由图象可知当直线y=x-1与抛物线相切时，此时z取得最小值，
将y=x-1代入x²=zy，得x²-zx+z=0，
由△=z²-4z=0得z=4或z=0（舍去），
故

的最小值是4，
故答案为：4

点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．

练习册系列答案

相关题目

，x∈[1，17]．
（1）证明函数f（x）在[1，17]上为增函数；
（2）求此函数的最大值和最小值．

如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2

．M是AD的中点．
（1）证明：平面ABC⊥平面ADC；
（2）若∠BDC=60°，求直线BM与CD所成的余弦值的大小．
（3）若∠BDC=60°，求二面角C-BM-D的大小．

设△ABC三个内角A、B、C所对的边分别为a，b，c．已知C=

，acosA=bcosB．
（1）求角A的大小；
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC=2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA=α，求PM+PN的最大值及此时α的取值．

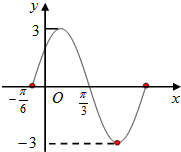如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

）的部分图象，
（1）求函数f（x）的解析式；
（2）当x∈(-

，0)时，求函数的值域．

设函数f（x）=lnx，有以下4个命题：
①对任意的x₁、x₂∈（0，+∞），有f(

x1+x2

)≤

f(x1)+f(x2)

；
②对任意的x₁、x₂∈（1，+∞），有f（x₁）-f（x₂）＜x₂-x₁；
③对任意的x₁、x₂∈（e，+∞），有x₁f（x₂）＜x₂f（x₁）；
④对任意的0＜x₁＜x₂，总有x₀∈（x₁，x₂），使得f(x0)≤

在0°～360°范围内，与1000°角终边相同的角：

．

已知m＞0，n＞0，且m+n=4，则mn的最大值是

．

试题分类