题目内容
等差数列{an}中,a3+a4+a5+a6+a7=150,则a2+a8= .
考点:等差数列的性质
专题:等差数列与等比数列
分析:由题意和等差数列的性质化简:a3+a4+a5+a6+a7=150,求出a5的值,代入a2+a8求值即可.
解答:
解:由题意知,a3+a4+a5+a6+a7=150,
则由等差数列的性质得,5a5=150,即a5=30,
所以a2+a8=2a5=60,
故答案为:60.
则由等差数列的性质得,5a5=150,即a5=30,
所以a2+a8=2a5=60,
故答案为:60.
点评:本题考查等差数列的性质的灵活运用,一定要注意项数之间的关系,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
我们把复数a-bi叫做复数z=a+bi(a,b∈R)的共轭复数,记作
,若i是虚数单位,z=1+i,
为复数z的共轭复数,则z•
+|
|-1=( )
. |
| z |
| • |
| z |
| • |
| z |
| • |
| z |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知函数f(x)=
,f2(x)=f(x),fn+1(x)=f(fn(x)),x∈N+,则f2015(x)=( )
| 1 |
| 1-x |
| A、x | ||
B、
| ||
C、
| ||
D、
|
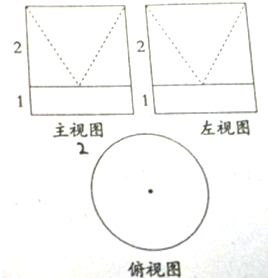 如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.
如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.