题目内容
已知数列{an}满足a1=
,(1-an)an+1=
.令bn=an-
.
(1)求证:数列{
}为等差数列;
(2)求和:Sn=
+
+…+
.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(1)求证:数列{
| 1 |
| bn |
(2)求和:Sn=
| a2 |
| a1 |
| a3 |
| a2 |
| an+1 |
| an |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)根据已知条件对关系式进行恒等变换,会进一步利用定义证明数列是等差数列.
(2)利用(1)的结论,进一步求出数列的通项公式,对关系式进行恒等变换,最后利用裂项相消法求出数列的和.
(2)利用(1)的结论,进一步求出数列的通项公式,对关系式进行恒等变换,最后利用裂项相消法求出数列的和.
解答:
解:(1)已知数列满足关系式:(1-an)an+1=
,
所以:1-an=
,
则:an-1=-
,
所以:an-
=
-
=
=
则:
=
=
=2+
由于:bn=an-
所以:bn+1=an+1-
-
=-2(常数)
所以:数列{
}是等差数列.
(2)由(1)得:
=
-2(n-1)
整理得:an=
(
)
所以:
=1+
=1+
(
-
)
Sn=
+
+…+
=(1+1+…+1)+
(1-
+
-
+…+
-
+
-
)
=n+
(1+
-
-
)
=n+
(
-
-
)
| 1 |
| 4 |
所以:1-an=
| 1 |
| 4an+1 |
则:an-1=-
| 1 |
| 4an+1 |
所以:an-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4an+1 |
| 2an+1-1 |
| 4an+1 |
2(an+1-
| ||
| 4an+1 |
则:
| 1 | ||
an-
|
| 2an+1 | ||
an+1-
|
| 2an+1-1+1 | ||
an+1-
|
| 1 | ||
an+1-
|
由于:bn=an-
| 1 |
| 2 |
所以:bn+1=an+1-
| 1 |
| 2 |
| 1 |
| bn+1 |
| 1 |
| bn |
所以:数列{
| 1 |
| bn |
(2)由(1)得:
| 1 | ||
an-
|
| 1 | ||
a1-
|
整理得:an=
| 1 |
| 2 |
| n |
| n+1 |
所以:
| an+1 |
| an |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
Sn=
| a2 |
| a1 |
| a3 |
| a2 |
| an+1 |
| an |
=(1+1+…+1)+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=n+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=n+
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
点评:本题考查的知识要点:递推关系式的恒等变换,利用定义法证明数列是等差数列,裂项相消法的应用.属于中等题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
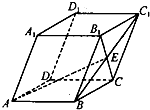 如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记
如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| AE |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|