题目内容
已知函数f(x)=
,f2(x)=f(x),fn+1(x)=f(fn(x)),x∈N+,则f2015(x)=( )
| 1 |
| 1-x |
| A、x | ||
B、
| ||
C、
| ||
D、
|
考点:抽象函数及其应用
专题:函数的性质及应用
分析:先分别求出f2∴、f3(x)、f4(x)、f5(x),推出f5(x)=f(f4(x))=f(x)=f2(x);
故f3k+n(x)=fn(x),则f2015(x)就可求出.
故f3k+n(x)=fn(x),则f2015(x)就可求出.
解答:
f2(x)=f(x)=
,∴f3(x)=f(f2(x))=
=
;f4(x)=f(f3(x))=
=x;
∴f5(x)=f(f4(x))=f(x)=f2(x);
f3k+n(x)=fn(x),
f2015(x)=f3×671+2(x))=f2(x)=f(x)=
,
故选:B.
| 1 |
| 1-x |
| 1 | ||
1-
|
| 1-x |
| -x |
| 1 | ||
1-
|
∴f5(x)=f(f4(x))=f(x)=f2(x);
f3k+n(x)=fn(x),
f2015(x)=f3×671+2(x))=f2(x)=f(x)=
| 1 |
| 1-x |
故选:B.
点评:本题主要考查函数的性质,从给定的条件中找出函数所满足的特点与规律,是做有关函数题的技巧.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知O是平面上任意一点,且
=
(
+
),则点C是AB的( )
| OC |
| 1 |
| 2 |
| OA |
| OB |
| A、三等分点 | B、中点 |
| C、四等分点 | D、无法判断 |
将号码分别为1,2,…,8的八个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,其号码为x,放回后乙从此袋中在摸出一个球,其中号码为y,则不等式x+2y-10<0成立的事件发生的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
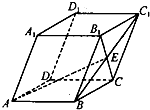 如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记
如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| AE |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|