题目内容

17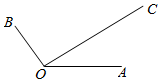．如图，平面内有三个向量$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$，其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°，且$|\overrightarrow{OA}|=2，|\overrightarrow{OC}|=4\sqrt{3}$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}（λ，μ∈R）$，则λ=4．

分析 以OC为对角线，以OA，OB方向为邻边作平行四边形，求出平行四边形OA方向上的边长即可得出答案．

解答 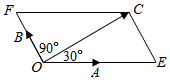解：过点C作CE∥OB交OA的延长线于点E，过点C作CF∥OA交OB的延长线于点F，则$\overrightarrow{OC}=\overrightarrow{OE}+\overrightarrow{OF}$．
∴∠OCE=∠COF=90°，∵∠COE=30°，∴CE=$\frac{1}{2}$OE，
∵CE2+OC2=OE2，∴CE=4，OE=8．
∵OA=2，∴λ=$\frac{OE}{OA}$=4．
故答案为：4．

点评 本题考查了平面向量的基本定理，向量运算的几何意义，属于基础题．

练习册系列答案
相关题目
10．已知sin（α-180°）-sin（270°-α）=m，则sin（180°+α）•sin（270°+α）用m表示为（　　）
A．$\frac{{m}^{2}-1}{2}$B．$\frac{{m}^{2}+1}{2}$C．$\frac{1{-m}^{2}}{2}$D．-$\frac{{m}^{2}+1}{2}$
8．（Ⅰ）求函数$y=\sqrt{2sinx+\sqrt{3}}$的定义域．
（Ⅱ）已知$sin（{540°}+α）=-\frac{4}{5}$，α为第二象限角．分别求cos（α-270°）及$\frac{{{{[sin（{{180}°}-α）+cos（{{360}°}-α）]}^2}}}{{tan（{{180}°}+α）}}$
的值．
5．计算下列积分：
（1）$\int_{-1}^2{|x-1|dx}$；
（2）$\int_0^1{\sqrt{1-{x^2}}dx}$．
12．一个几何体的三视图如图所示，其中正视图是正三角形，则几何体的表面积为（　　）
A．$4（1+\sqrt{3}+\sqrt{7}）$B．$4（\sqrt{3}+\sqrt{7}）$C．$8（1+\sqrt{3}+\sqrt{7}）$D．$8（\sqrt{3}+\sqrt{7}）$
2．一个几何体的三视图如图所示，那么此几何体的侧面积（单位：cm2）为（　　）
A．120B．80C．64D．48
9．6把椅子摆成一排，3人就座，三人全相邻的坐法种数为（　　）
A．18B．24C．48D．72
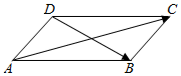6．已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为30°，且$|{\overrightarrow a}|$=$\sqrt{3}$，$|{\overrightarrow b}|$=1．
（1）求$\overrightarrow a•\overrightarrow b$；
（2）求$|{\overrightarrow a-\overrightarrow b}|$的值；
（3）如图，设向量$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，\overrightarrow{AC}=\overrightarrow p，\overrightarrow{DB}=\overrightarrow q$，求向量$\overrightarrow p$在$\overrightarrow{q}$方向上的投影．
7．${3^{-2}}，{2^{\frac{1}{3}}}，{log_{\frac{1}{2}}}3$三个数中最大的数是${2}^{\frac{1}{3}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网