题目内容
9．6把椅子摆成一排，3人就座，三人全相邻的坐法种数为（ ）| A． | 18 | B． | 24 | C． | 48 | D． | 72 |
分析 把3人捆绑在一起看做一个复合元素，插入到3空把椅子所形成的4个空中即可．
解答 解：把3人捆绑在一起看做一个复合元素，插入到3把空椅子所形成的4个空中，故有A33A41=24种，
故选：B．
点评 本题考查计数原理的运用，考查捆绑法，插空法，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
2．函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为π，且其图象经过点（$\frac{7π}{12}$，0），则函数f（x）在区间[0，$\frac{π}{2}$]上的最大值与最小值的和为（ ）
| A． | 1-$\frac{\sqrt{3}}{2}$ | B． | 0 | C． | $\frac{1}{2}$ | D． | 1+$\frac{\sqrt{3}}{2}$ |
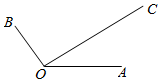如图，平面内有三个向量$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$，其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°，且$|\overrightarrow{OA}|=2，|\overrightarrow{OC}|=4\sqrt{3}$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}（λ，μ∈R）$，则λ=4．
14．已知函数g（x）满足g（x）=g′（1）ex-1-g（0）x+$\frac{1}{2}{x}^{2}$，且存在实数x0使得不等式2m-1≥g（x0）成立，则m的取值范围为（ ）
| A． | （-∞，2] | B． | （-∞，3] | C． | [1，+∞） | D． | [0，+∞） |
18．在空间直角坐标系O-xyz中，点A（1，2，3）关于z轴的对称点为（ ）
| A． | （-1，-2，3） | B． | （-1，2，3） | C． | （-1，-2，-3） | D． | （1，2，-3） |