题目内容
2.一个几何体的三视图如图所示,那么此几何体的侧面积(单位:cm2)为( )
| A. | 120 | B. | 80 | C. | 64 | D. | 48 |
分析 由已知中的三视图可得该几何体是一个四棱锥,结合棱锥的侧面积公式,进而可得答案.
解答 解:由已知中的三视图可得该几何体是一个四棱锥,
棱锥的底面边长为8cm,侧面的高为5cm,
故棱锥的侧面积为:4×$\frac{1}{2}$×8×5=80cm2,
故选:B.
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
13.若曲线y=e2x的一条切线l与直线x+2y-8=0垂直,则l的方程为( )
| A. | y=$\frac{1}{2}$x+1 | B. | y=-2x+1 | C. | y=2x-1 | D. | y=2x+1 |
7.一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
从第一个学生开始买饭时计时.
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)X表示至第2分钟末已买完饭的人数,求X的分布列及数学期望.
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)X表示至第2分钟末已买完饭的人数,求X的分布列及数学期望.
14.已知函数g(x)满足g(x)=g′(1)ex-1-g(0)x+$\frac{1}{2}{x}^{2}$,且存在实数x0使得不等式2m-1≥g(x0)成立,则m的取值范围为( )
| A. | (-∞,2] | B. | (-∞,3] | C. | [1,+∞) | D. | [0,+∞) |
12.已知集合A={x|2x+1<0},B={x|-1<x<0},那么A∩B=( )
| A. | $\{x|-1<x<-\frac{1}{2}\}$ | B. | {x|x<0} | C. | $\{x|x<-\frac{1}{2}\}$ | D. | $\{x|-\frac{1}{2}<x<0\}$ |
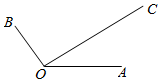 如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.
如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.