题目内容
8.(Ⅰ)求函数$y=\sqrt{2sinx+\sqrt{3}}$的定义域.(Ⅱ)已知$sin({540°}+α)=-\frac{4}{5}$,α为第二象限角.分别求cos(α-270°)及$\frac{{{{[sin({{180}°}-α)+cos({{360}°}-α)]}^2}}}{{tan({{180}°}+α)}}$
的值.
分析 (Ⅰ)由题意可得$2sinx+\sqrt{3}≥0$,解得$-\frac{π}{3}+2kπ≤x≤\frac{4π}{3}+2kπ$(k∈Z),从而可求定义域.
(Ⅱ)由已知利用诱导公式可得$sinα=\frac{4}{5}$,利用诱导公式可得cos(α-270°)的值,根据角的范围,利用同角三角函数基本关系式可求cosα,利用诱导公式化简所求即可计算得解.
解答 解:(Ⅰ)由题意可得:$2sinx+\sqrt{3}≥0$,即$sinx≥-\frac{{\sqrt{3}}}{2}$,
解得(图象法或单位圆法):$-\frac{π}{3}+2kπ≤x≤\frac{4π}{3}+2kπ$(k∈Z),
∴所求定义域为[$-\frac{π}{3}+2kπ,\frac{4π}{3}+2kπ$](k∈Z)
(Ⅱ)由已知$sin({540°}+α)=-\frac{4}{5}$,可得$sinα=\frac{4}{5}$,
∴cos(α-270°)=$-sinα=-\frac{4}{5}$,
又∵α为第二象限角,
∴$cosα=-\frac{3}{5}$,
于是:$\frac{{{{[sin({{180}°}-α)+cos({{360}°}-α)]}^2}}}{{tan({{180}°}+α)}}$=$\frac{{{{(sinα+cosα)}^2}}}{tanα}=-\frac{3}{100}$.
点评 本题主要考查了三角函数定义域及其求法,考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知直线l1:x+ay-1=0,直线l2:ax+(a-2)y+3=0,其中a∈R,则“a=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象经过点($\frac{7π}{12}$,0),则函数f(x)在区间[0,$\frac{π}{2}$]上的最大值与最小值的和为( )
| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
13.若曲线y=e2x的一条切线l与直线x+2y-8=0垂直,则l的方程为( )
| A. | y=$\frac{1}{2}$x+1 | B. | y=-2x+1 | C. | y=2x-1 | D. | y=2x+1 |
18.在空间直角坐标系O-xyz中,点A(1,2,3)关于z轴的对称点为( )
| A. | (-1,-2,3) | B. | (-1,2,3) | C. | (-1,-2,-3) | D. | (1,2,-3) |
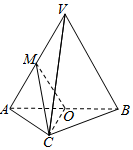 如图,在三棱锥V-ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点.
如图,在三棱锥V-ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点.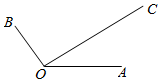 如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.
如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.