题目内容
6. 已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为30°,且$|{\overrightarrow a}|$=$\sqrt{3}$,$|{\overrightarrow b}|$=1.
已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为30°,且$|{\overrightarrow a}|$=$\sqrt{3}$,$|{\overrightarrow b}|$=1.(1)求$\overrightarrow a•\overrightarrow b$;
(2)求$|{\overrightarrow a-\overrightarrow b}|$的值;
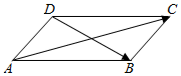
(3)如图,设向量$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AC}=\overrightarrow p,\overrightarrow{DB}=\overrightarrow q$,求向量$\overrightarrow p$在$\overrightarrow{q}$方向上的投影.
分析 (1)直接由已知结合数量积公式求解;
(2)利用$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=(\overrightarrow{a}-\overrightarrow{b})^{2}$,等式右边展开后代入数量积得答案;
(3)由$\overrightarrow{p}=\overrightarrow{a}+\overrightarrow{b},\overrightarrow{q}=\overrightarrow{a}-\overrightarrow{b}$,代入投影公式化简即可.
解答 解:向量$\overrightarrow a$与$\overrightarrow b$的夹角为30°,且$|{\overrightarrow a}|$=$\sqrt{3}$,$|{\overrightarrow b}|$=1.
(1)$\overrightarrow a•\vec b=|{\overrightarrow a}|•|{\vec b}|cos{30°}=\sqrt{3}×1×\frac{{\sqrt{3}}}{2}=\frac{3}{2}$;
(2)$|{\overrightarrow a-\vec b}|=\sqrt{{{({\overrightarrow a-\vec b})}^2}}=\sqrt{{{\overrightarrow a}^2}-2\overrightarrow a•\vec b+{{\vec b}^2}}=\sqrt{3-3+1}=1$;
(3)∵$\overrightarrow{p}=\overrightarrow{a}+\overrightarrow{b},\overrightarrow{q}=\overrightarrow{a}-\overrightarrow{b}$,
∴$\frac{\vec p•\vec q}{{|{\vec q}|}}=\frac{{{{\overrightarrow a}^2}-{{\vec b}^2}}}{{\sqrt{(\overrightarrow a-\vec b{)^2}}}}=\frac{3-1}{{\sqrt{{{\overrightarrow a}^2}-2\overrightarrow a•\vec b+{{\vec b}^2}}}}=\frac{2}{{\sqrt{3-3+1}}}=2$.
点评 本题考查平面向量的数量积运算,考查向量模的求法,对于(3)的求解,需要掌握向量在向量方向上的投影的概念,是中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | (-∞,2] | B. | (-∞,3] | C. | [1,+∞) | D. | [0,+∞) |
| A. | (-1,-2,3) | B. | (-1,2,3) | C. | (-1,-2,-3) | D. | (1,2,-3) |
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 若命题p:?x∈R,x2-2x-1>0,则命题¬p:?x∈R,x2-2x-1<0 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “b2=ac”是“a,b,c成等比数列”的充要条件 |
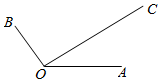 如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.
如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.