题目内容
10.已知sin(α-180°)-sin(270°-α)=m,则sin(180°+α)•sin(270°+α)用m表示为( )| A. | $\frac{{m}^{2}-1}{2}$ | B. | $\frac{{m}^{2}+1}{2}$ | C. | $\frac{1{-m}^{2}}{2}$ | D. | -$\frac{{m}^{2}+1}{2}$ |
分析 由已知利用诱导公式可得sin$αcosα=\frac{1-{m}^{2}}{2}$.再利用诱导公式得到sin(180°+α)•sin(270°+α)=-sinα•(-cosα)=sinαcosα得答案.
解答 解:由sin(α-180°)-sin(270°-α)=m,得:
-sinα+cosα=m,即sinα-cosα=-m,
两边平方得,sin2α-2sinαcosα+cos2α=m2,
∴sin$αcosα=\frac{1-{m}^{2}}{2}$.
∴sin(180°+α)•sin(270°+α)=-sinα•(-cosα)=sinαcosα=$\frac{1-{m}^{2}}{2}$.
故选:C.
点评 本题考查三角函数的化简与求值,主要考查了诱导公式的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知直线l1:x+ay-1=0,直线l2:ax+(a-2)y+3=0,其中a∈R,则“a=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.在△ABC中M是BC的中点,BC=8,AM=3,AM⊥BC,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )
| A. | -7 | B. | -$\frac{7}{2}$ | C. | 0 | D. | 7 |
2.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象经过点($\frac{7π}{12}$,0),则函数f(x)在区间[0,$\frac{π}{2}$]上的最大值与最小值的和为( )
| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
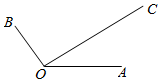 如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.
如图,平面内有三个向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且$|\overrightarrow{OA}|=2,|\overrightarrow{OC}|=4\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则λ=4.