题目内容
数列{an}中，若a1=1，a2=3且an+2=an+1-an（n∈N*），则a16=（ ）
| A、-1 | B、1 | C、2 | D、3 |
考点：数列递推式
专题：概率与统计
分析：由已知条件利用递推思想求出数列的前8项，从而得到数列{an}是周期为6的周期数列，由此能求出结果．
解答：
解：∵数列{an}中，a1=1，a2=3且an+2=an+1-an（n∈N*），
∴a3=3-1=2，
a4=2-3=-1，
a5=-1-2=-3，
a6=-3+1=-2，
a7=-2+3=1，
a8=1+2=3，
∴数列{an}是周期为6的周期数列，
∵16=2×6+4，
∴a16=a4=-1．
故选：A．
∴a3=3-1=2，
a4=2-3=-1，
a5=-1-2=-3，
a6=-3+1=-2，
a7=-2+3=1，
a8=1+2=3，
∴数列{an}是周期为6的周期数列，
∵16=2×6+4，
∴a16=a4=-1．
故选：A．
点评：本题考查数列的第16项的求法，是基础题，解题时要注意递推思想的合理运用．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
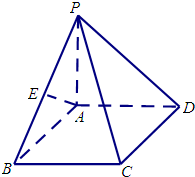如图，在四棱锥P-ABCD中，地面ABCD为正方形，PA⊥地面ABCD，AB=AP=1，E为PB的中点．
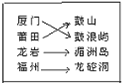福州、厦门、莆田、龙岩四个城市，它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞，把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列，现在一名旅游爱好者随机用4条线把左右全部连接起来，构成“一一对应”，已知连对的得2分，连错的得0分（如图所示是一种“一一对应”的连法，连对的只有一个“厦门→鼓浪屿”）．设函数f（x）（x∈R）满足f（x+1）=-f（x）对任意实数x恒成立，且x∈[0，1]时，f（x）=（x-1）2．那么函数y=f（x）-sinx在区间[0，10]上的零点个数有（ ）个．
| A、6 | B、7 | C、8 | D、9 |
函数f（x）=|log0.5x|-
的零点个数为（ ）
| 1 |
| 2x |
| A、1 | B、2 | C、3 | D、4 |