题目内容
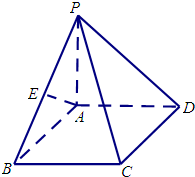 如图,在四棱锥P-ABCD中,地面ABCD为正方形,PA⊥地面ABCD,AB=AP=1,E为PB的中点.
如图,在四棱锥P-ABCD中,地面ABCD为正方形,PA⊥地面ABCD,AB=AP=1,E为PB的中点.(1)证明:AE⊥平面PBC;
(2)求三棱锥D-BPC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知得AE⊥PB,平面ABP⊥平面ABCD,BC⊥平面ABP,AE⊥BC,由此能证明AE⊥平面PBC.
(2)由已知得VD-EPC=VA-EPC,从而VA-EPC=
S△PBC•AE,由此能求出三棱锥D-BPC的体积.
(2)由已知得VD-EPC=VA-EPC,从而VA-EPC=
| 1 |
| 3 |
解答:
(1)证明:∵AB=AP,E为PB的中点,
∴AE⊥PB,
∵AP⊥平面ABCD,∴平面ABP⊥平面ABCD,
又BC⊥AB,∴BC⊥平面ABP,
∵AE?平面ABP,∴AE⊥BC,
∵PB,BC?平面ABP,
∴AE⊥平面PBC.
(2)解:∵AD∥BC,AD?面SBC,BC?平面SBC,
∴AD∥平面SBC,
∴VD-EPC=VA-EPC,
又∵AE⊥平面PBC,
∴VA-EPC=
S△PBC•AE=
×
×1×
×
=
,
∴三棱锥D-BPC的体积是
.
∴AE⊥PB,
∵AP⊥平面ABCD,∴平面ABP⊥平面ABCD,
又BC⊥AB,∴BC⊥平面ABP,
∵AE?平面ABP,∴AE⊥BC,
∵PB,BC?平面ABP,
∴AE⊥平面PBC.
(2)解:∵AD∥BC,AD?面SBC,BC?平面SBC,
∴AD∥平面SBC,
∴VD-EPC=VA-EPC,
又∵AE⊥平面PBC,
∴VA-EPC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 | ||
|
| 1 |
| 6 |
∴三棱锥D-BPC的体积是
| 1 |
| 6 |
点评:本题考查直线与平面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则称点对[P、Q]是函数y=f(x)的一对“友好点对”(点对[P、Q]与[Q、P]看作同一对“友好点对”).已知函数f(x)=
则此函数的“友好点对”有( )
|
| A、4对 | B、3对 | C、2对 | D、1对 |
一个棱柱至少有( )个面,面数最少的一个棱锥有( )个顶点,顶点最少的一个棱台有( )条侧棱.
| A、8 4 6 |
| B、5 4 3 |
| C、4 4 4 |
| D、4 6 3 |
数列{an}中,若a1=1,a2=3且an+2=an+1-an(n∈N*),则a16=( )
| A、-1 | B、1 | C、2 | D、3 |