题目内容
已知α,β是二个不同的平面,m,n是二条不同直线,给出下列命题:
①若m∥n,m⊥α,则n⊥α;
②若m∥α,α∩β=n则m⊥n;
③若m⊥α,m⊥β则α∥β;
④若m⊥α,m?β,则α⊥β,
真命题共有( )
①若m∥n,m⊥α,则n⊥α;
②若m∥α,α∩β=n则m⊥n;
③若m⊥α,m⊥β则α∥β;
④若m⊥α,m?β,则α⊥β,
真命题共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:分别根据空间直线和平面平行或垂直的判定定理和性质定理进行判断即可.
解答:
解:①根据线面垂直的性质可知若m∥n,m⊥α,则n⊥α成立,故①正确;
②若m∥α,α∩β=n则m⊥n不成立,故②错误;
③根据线面垂直的性质可知若m⊥α,m⊥β则α∥β成立,故③正确;
④根据面面垂直的判定定理可知若m⊥α,m?β,则α⊥β成立,故④正确,
故真命题有①③④,
故选:C
②若m∥α,α∩β=n则m⊥n不成立,故②错误;
③根据线面垂直的性质可知若m⊥α,m⊥β则α∥β成立,故③正确;
④根据面面垂直的判定定理可知若m⊥α,m?β,则α⊥β成立,故④正确,
故真命题有①③④,
故选:C
点评:本题主要考查命题的真假判断,根据空间直线的位置关系是解决本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
函数f(x)=|4sin(2x+(
))|的最小正周期为( )
| π |
| 6 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
若f(x)=
,则f(-2)=( )
|
| A、-2 | B、1 | C、2 | D、3 |
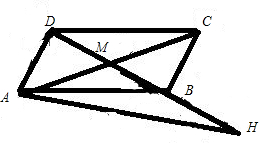 如图,平行四边形ABCD的两条对角线相交于点M,
如图,平行四边形ABCD的两条对角线相交于点M,