题目内容
若f（x）=
，则f（-2）=（ ）
|
| A、-2 | B、1 | C、2 | D、3 |
考点：抽象函数及其应用,分段函数的应用
专题：函数的性质及应用
分析：根据自变量的不同取值，适当选取分段函数的表达式，代入即可得到结论．
解答：
解：∵-2＜0，∴f（-2）=f（-2+1）+1=f（-1）+1，
又f（-1）=f（-1+1）+1=f（0）+1=f（0+1）+1+1=f（1）+2；
∴f（-2）=f（-1）+1=f（1）+3，
∵f（1）=lg1=0，
∴f（-2）=0+3=3
故选：D．
又f（-1）=f（-1+1）+1=f（0）+1=f（0+1）+1+1=f（1）+2；
∴f（-2）=f（-1）+1=f（1）+3，
∵f（1）=lg1=0，
∴f（-2）=0+3=3
故选：D．
点评：本题主要考查函数值的计算，根据分段函数的表达式以及对数的运算是解决本题的关键．
练习册系列答案
相关题目
已知α，β是二个不同的平面，m，n是二条不同直线，给出下列命题：
①若m∥n，m⊥α，则n⊥α；
②若m∥α，α∩β=n则m⊥n；
③若m⊥α，m⊥β则α∥β；
④若m⊥α，m?β，则α⊥β，
真命题共有（ ）
①若m∥n，m⊥α，则n⊥α；
②若m∥α，α∩β=n则m⊥n；
③若m⊥α，m⊥β则α∥β；
④若m⊥α，m?β，则α⊥β，
真命题共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
若
、
是平面内的一组基底，则下列四组向量能作为平面向量的基底的是（ ）
| e1 |
| e2 |
A、
| ||||||||||
B、2
| ||||||||||
C、2
| ||||||||||
D、
|
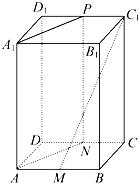如图，长方体ABCD-A1B1C1D1中，M，N，P分别为线段AB，CD，C1D1的中点．求证：