题目内容

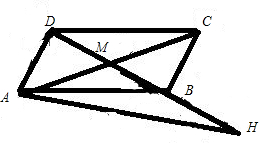如图，平行四边形ABCD的两条对角线相交于点M，
AB
=
a
，
AD
=
b
，在DB延长线上取点H，使BH=MB，若
AH
=λ1
a
+λ2
b
，则λ1=
 
，λ2=
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：根据平面向量的基本定理进行分解即可得到结论．
解答： 解：∵在DB延长线上取点H，使BH=MB，
∴DH=3BH，即DH=
3
2
DB，则
DH
=
3
2
DB
，
则
AH
=
AD
+
DH
=
AD
+
3
2
DB
═
AD
+
3
2
（
AB
-
AD
）=
3
2
AB
-
1
2
AD
=
3
2
a
-
1
2
b
，
∵
AH
=λ1
a
AH
=λ1
a
+λ2
b
，
∴λ1=
3
2
，λ2=
1
2
，
故答案为：
3
2
，
1
2
点评：本题主要考查平面向量的基本定理的应用，比较基础．
练习册系列答案
相关题目
一动圆过定点A（1，0），且与定圆（x+1）2+y2=16相切，则动圆圆心轨迹方程是
 
．
设A={x|-2＜x≤2}，B={x|0≤x≤4}，求A∩B．
一个复数Z若满足Zn=1，n，m是正整数，m＜n时Zm≠1，则称Z为n次本原单位根，则四次原单位根有
 
．
如图所示在棱长为1的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．
（1）求证：EF∥平面ABC1D1；
（2）求证：B1C⊥平面ABC1D1；
（3）设四棱锥B1-ABC1D1的体积为V1，正方体ABCD-A1B1C1D1的体积为V2，求
V1
V2
．
根据下列条件，求出数列的通项公式．
（1）a1=2，an=an-1+2n-1（n≥2）；
（2）a1=1，（n+1）an+12-nan2+an+1an=0且an＞0；
（3）a1=1，an+1=2an+3．
已知α，β是二个不同的平面，m，n是二条不同直线，给出下列命题：
①若m∥n，m⊥α，则n⊥α；
②若m∥α，α∩β=n则m⊥n；
③若m⊥α，m⊥β则α∥β；
④若m⊥α，m?β，则α⊥β，
真命题共有（　　）
A、1个B、2个C、3个D、4个
若
e1
、
e2
是平面内的一组基底，则下列四组向量能作为平面向量的基底的是（　　）
A、
e1
-
e2
，
e2
-
e1
B、2
e1
-
e2
，
e1
-
1
2
e2
C、2
e2
-3
e1
，6
e1
-4
e2
D、
e1
+
e2
，
e1
-
e2
已知
a
=（sinθ，cosθ，
2
），
b
=（cosθ，sinθ，
2
2
），且
a
⊥
b
，则θ=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网