题目内容
已知M是所有同时满足下列性质的函数f(x)的集合:
①函数f(x)在其定义域是单调函数;
②在函数f(x)的定义域内存在区间[a,b],使得f(x)在[a,b]上的最小值是a,最大值是b.
(1)判断函数f(x)=x2,x∈[0,+∞)是否属于集合M?若是,请求出相应的区间[a,b];若不是,请说明理由;
(2)证明:函数f(x)=3log2x属于集合M;
(3)若函数f(x)=
属于M,求实数m的取值范围.
①函数f(x)在其定义域是单调函数;
②在函数f(x)的定义域内存在区间[a,b],使得f(x)在[a,b]上的最小值是a,最大值是b.
(1)判断函数f(x)=x2,x∈[0,+∞)是否属于集合M?若是,请求出相应的区间[a,b];若不是,请说明理由;
(2)证明:函数f(x)=3log2x属于集合M;
(3)若函数f(x)=
| mx |
| 1+|x| |
考点:对数函数图象与性质的综合应用
专题:计算题,函数的性质及应用
分析:(1)易知函数f(x)=x2在[0,+∞)上单调递增,再求解f(x)-x=x2-x=0,从而得到区间为[0,1];
(2)先证明单调性,再作图说明F(x)=3log2x-x有两个零点即可;
(3)由于函数f(x)=
在R上连续,且是奇函数,故只需f(x)=
在[0,+∞)上单调,且有区间即可;求导确定单调性,令H(x)=
-x=
=0求解.
(2)先证明单调性,再作图说明F(x)=3log2x-x有两个零点即可;
(3)由于函数f(x)=
| mx |
| 1+|x| |
| mx |
| 1+|x| |
| mx |
| 1+|x| |
| -x(x-m+1) |
| 1+x |
解答:
解:(1)易知函数f(x)=x2在[0,+∞)上单调递增,
令f(x)-x=x2-x=0,
解得,x=0或x=1;
故区间为[0,1];
故函数f(x)=x2,x∈[0,+∞)属于集合M;
(2)证明:函数f(x)=3log2x在其定义域(0,+∞)上单调递增,
令F(x)=3log2x-x,
其图象如下,
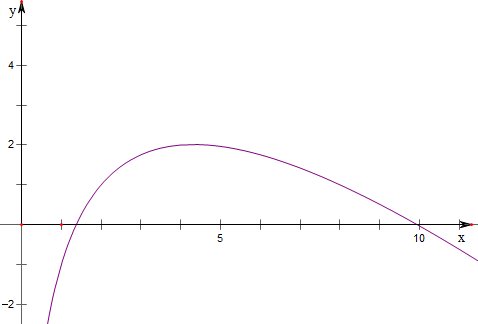
故其与x轴的交点可作为a,b;
故函数f(x)=3log2x属于集合M;
(3)函数f(x)=
在R上连续,且是奇函数,
故只需f(x)=
在[0,+∞)上单调,
则f′(x)=
,
故m≠0;
f(0)=0,
H(x)=
-x=
=0,
故,m-1>0,
故m>1.
令f(x)-x=x2-x=0,
解得,x=0或x=1;
故区间为[0,1];
故函数f(x)=x2,x∈[0,+∞)属于集合M;
(2)证明:函数f(x)=3log2x在其定义域(0,+∞)上单调递增,
令F(x)=3log2x-x,
其图象如下,

故其与x轴的交点可作为a,b;
故函数f(x)=3log2x属于集合M;
(3)函数f(x)=
| mx |
| 1+|x| |
故只需f(x)=
| mx |
| 1+|x| |
则f′(x)=
| m |
| (1+x)2 |
故m≠0;
f(0)=0,
H(x)=
| mx |
| 1+|x| |
| -x(x-m+1) |
| 1+x |
故,m-1>0,
故m>1.
点评:本题考查了函数的单调性的判断及零点的判断,同时考查了函数的图象的应用,属于中档题.

练习册系列答案
相关题目
动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A、y=
| ||
| B、y=kx(x≠0) | ||
C、y=-
| ||
| D、y=±kx(x≠0) |