题目内容
设函数f(x)=sinx•cosx-
cos(π+x)•cosx(x∈R).
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象向右、向上分别平移
、
个单位长度得到y=g(x)的图象,求y=g(x)在(0,
]的值域.
| 3 |
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象向右、向上分别平移
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
考点:二倍角的正弦,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值
分析:(1)利用倍角公式、两角和差的正弦公式、周期公式即可得出;
(2)利用三角函数变换可得y=g(x)=sin(2(x-
)+
)+
+
=sin(2x-
)+
,再利用正弦函数的单调性即可得出.
(2)利用三角函数变换可得y=g(x)=sin(2(x-
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 6 |
| 3 |
解答:
解:(1)函数f(x)=sinx•cosx-
cos(π+x)•cosx=
sin2x+
=sin(2x+
)+
.
∴T=
=π.
(2)函数y=f(x)的图象向右、向上分别平移
、
个单位长度得到y=g(x)=sin(2(x-
)+
)+
+
=sin(2x-
)+
.
∵x∈(0,
],∴(2x-
)∈(-
,
],
∴sin(2x-
)∈(-
,
],
∴g(x)∈(
-
,
].
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 3 |
| ||
| 2 |
∴T=
| 2π |
| 2 |
(2)函数y=f(x)的图象向右、向上分别平移
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 6 |
| 3 |
∵x∈(0,
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
∴g(x)∈(
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
点评:本题考查了倍角公式、两角和差的正弦公式、周期公式、三角函数变换、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
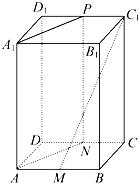 如图,长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点.求证:
如图,长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点.求证: