题目内容
若不等式x3-mx2+x+m-2≤0在x∈(1,+∞)有解,则实数m的取值范围是 .
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用,不等式的解法及应用
分析:运用参数分离可得,m≥
,令t=x+1(t>2),则y=
=t+
-1,运用导数判断右边的单调性,得到范围即可.
| x3+x-2 |
| x2-1 |
| (t-1)2+t+1 |
| t |
| 2 |
| t |
解答:
解:由于x>1,则不等式x3-mx2+x+m-2≤0,
即为m≥
=
,
令t=x+1(t>2),则y=
=t+
-1,y′=1-
>0,则y在t>2递增,即有y>2,
则不等式在x∈(1,+∞)有解等价为m>2.
故答案为:(2,+∞).
即为m≥
| x3+x-2 |
| x2-1 |
| x2+x+2 |
| x+1 |
令t=x+1(t>2),则y=
| (t-1)2+t+1 |
| t |
=t+
| 2 |
| t |
| 2 |
| t2 |
则不等式在x∈(1,+∞)有解等价为m>2.
故答案为:(2,+∞).
点评:本题考查不等式有解的问题转化为求函数的最值,考查运用导数判断单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A、y=
| ||
| B、y=kx(x≠0) | ||
C、y=-
| ||
| D、y=±kx(x≠0) |
 如图所示在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
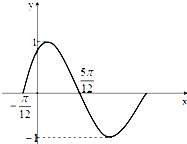 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<