题目内容
复数z=m2+5m+6+（m2-2m-15）i．
（Ⅰ）实数m取什么数值时，复数z为纯虚数；
（Ⅱ）当m=-4时，复数z0=z+a+（a-5）i（a∈R），求复数z0的模的最小值．
（Ⅰ）实数m取什么数值时，复数z为纯虚数；
（Ⅱ）当m=-4时，复数z0=z+a+（a-5）i（a∈R），求复数z0的模的最小值．
考点：复数代数形式的乘除运算
专题：计算题,数系的扩充和复数
分析：（Ⅰ）由纯虚数的定义可得方程，解出即可；
（Ⅱ）m=-4时，表示出z0，|z0|，利用二次函数的性质可求；
（Ⅱ）m=-4时，表示出z0，|z0|，利用二次函数的性质可求；
解答：
解：（I）∵z为纯虚数，
∴
，
解得
，
∴m=-2，
（II）m=-4时，z=2+9i，z0=z+a+（a-5）i=（2+a）+（a+4）i，
|z0|=
=
=
≥
，
∴复数z0的模的最小值为
．
∴
|
解得
|
∴m=-2，
（II）m=-4时，z=2+9i，z0=z+a+（a-5）i=（2+a）+（a+4）i，
|z0|=
| (2+a)2+(a+4)2 |
| 2a2+12a+20 |
| 2(a+3)2+2 |
| 2 |
∴复数z0的模的最小值为
| 2 |
点评：该题考查复数的基本概念、代数形式的乘除运算及复数的模，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知奇函数f（x）在[-1，0]上为单调递减函数，又α、β为锐角三角形两内角且α＞β，则下列结论正确的是（ ）
| A、f（cos α）＞f（cos β） |
| B、f（sin α）＞f（sin β） |
| C、f（sin α）＞f（cos β） |
| D、f（sin α）＜f（cos β） |
设z1，z2为复数，则下列四个结论中正确的是（ ）
| A、若z12+z22＞0，则z12＞-z22 | ||
B、|z1-z2|=
| ||
| C、z12+z22=0?z1=z2=0 | ||
D、z1-
|
设x，y满足的约束条件是
，则z=x+2y的最小值是（ ）
|
| A、-1 | B、3 | C、5 | D、6 |
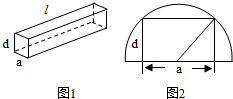如图1所示，一根水平放置的长方体枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．
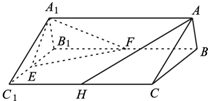如图，在直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，E、F分别是棱B1C1、B1B的中点，H在棱CC1上，且AB⊥AH．
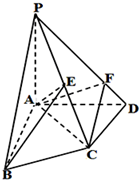如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC=3