题目内容
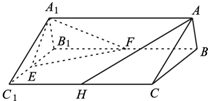 如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.(Ⅰ)求证:AB⊥平面AA1C1C;
(Ⅱ)求三棱锥A1-B1EF的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明AB⊥平面AA1C1C,只需证明AA1⊥AB,AB⊥AH;
(Ⅱ)求三棱锥A1-B1EF的体积,只需求VF-A1B1E.
(Ⅱ)求三棱锥A1-B1EF的体积,只需求VF-A1B1E.
解答:
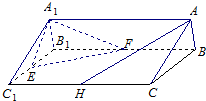 (Ⅰ)证明:∵在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC
(Ⅰ)证明:∵在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC
∴AA1⊥AB,…(2分)
又∵AB⊥AH,AA1∩AH=A,∴AB⊥平面AA1C1C…(5分)
(Ⅱ)解:由(Ⅰ)知:∠B1A1C1=90°
∵AB=AC=1,BB1=2,∴S△A1B1C1=
•1•1=
∵E、F分别是棱B1C1、B1B的中点,BB1=2,
∴S△A1B1E=
,B1F=1…(8分)
又∵BB1⊥平面A1B1C1,
∴三棱锥A1-B1EF的体积为VF-A1B1E=
•
•1=
…(12分)
 (Ⅰ)证明:∵在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC
(Ⅰ)证明:∵在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC∴AA1⊥AB,…(2分)
又∵AB⊥AH,AA1∩AH=A,∴AB⊥平面AA1C1C…(5分)
(Ⅱ)解:由(Ⅰ)知:∠B1A1C1=90°
∵AB=AC=1,BB1=2,∴S△A1B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
∵E、F分别是棱B1C1、B1B的中点,BB1=2,
∴S△A1B1E=
| 1 |
| 4 |
又∵BB1⊥平面A1B1C1,
∴三棱锥A1-B1EF的体积为VF-A1B1E=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
点评:本小题主要考查直线和直线、直线和平面的垂直关系、几何体的体积等基础知识,考查空间想象能力、运算求解能力、推理论证能力,考查了数形结合和化归与转化的数学思想方法.

练习册系列答案
相关题目
下列命题中为真命题的是( )
| A、?x∈R,x2+1<0 |
| B、?x∈Z,3x+1是整数 |
| C、?x∈R,|x|>3 |
| D、?x∈Q,x2∈Z |
图中阴影部分区域所表示的不等式组是( )


A、
| |||||
B、
| |||||
C、
| |||||
D、
|
设等差数列{an}的前n项和为Sn,若S3=9,S9=36,则a7+a8+a9等于( )
| A、15 | B、12 | C、36 | D、27 |
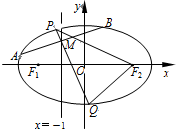 如图,F1、F2是离心率为
如图,F1、F2是离心率为