题目内容
设an=1+
+
+…+
(n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切自然数都成立,并试用数学归纳法证明你的结论.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:数学归纳法,数列递推式
专题:点列、递归数列与数学归纳法
分析:假设存在一次函数g(x)=kx+b(k≠0),依题意可求得k=1,b=0,故猜想:g(x)=x;然后用数学归纳法加以证明即可.
解答:
解:假设存在一次函数g(x)=kx+b(k≠0),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切自然数都成立,
则当n=2时有,a1=g(2)(a2-1),又∵a1=1,a2=1+
,∴g(2)=2即2k+b=2…①.
当n=3时有,a1+a2=g(3)(a3-1),又∵a1=1,a2=1+
,a2=1+
+
,∴g(3)=3,即3k+b=3…②,
由①②可得k=1,b=0,
所以猜想:g(x)=x,…(5分)
下面用数学归纳法加以证明:
(1)当n=2时,已经得到证明;…(6分)
(2)假设当n=k(k≥2,k∈N)时,结论成立,即存在g(k)=k,使得a1+a2+a3+…+ak-1=g(k)(ak-1)对k≥2的一切自然数都成立,则
当n=k+1时,a1+a2+a3+…+ak=(a1+a2+a3+…+ak-1)+ak=k(ak-1)+ak=(k+1)ak-k,…(8分)
又∵ak+1=1+
+
+…+
+
=ak+
,
∴ak=ak+1-
,
∴a1+a2+a3+…+ak=(k+1)(ak+1-
)-k=(k+1)(ak+1-1),
∴当n=k+1时,命题成立.…(11分)
由(1)(2)知,对一切n,(n≥2,n∈N*)有g(n)=n,使得a1+a2+a3+…+an-1=g(n)(an-1)都成立.…(12分)
则当n=2时有,a1=g(2)(a2-1),又∵a1=1,a2=1+
| 1 |
| 2 |
当n=3时有,a1+a2=g(3)(a3-1),又∵a1=1,a2=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
由①②可得k=1,b=0,
所以猜想:g(x)=x,…(5分)
下面用数学归纳法加以证明:
(1)当n=2时,已经得到证明;…(6分)
(2)假设当n=k(k≥2,k∈N)时,结论成立,即存在g(k)=k,使得a1+a2+a3+…+ak-1=g(k)(ak-1)对k≥2的一切自然数都成立,则
当n=k+1时,a1+a2+a3+…+ak=(a1+a2+a3+…+ak-1)+ak=k(ak-1)+ak=(k+1)ak-k,…(8分)
又∵ak+1=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| k+1 |
∴ak=ak+1-
| 1 |
| k+1 |
∴a1+a2+a3+…+ak=(k+1)(ak+1-
| 1 |
| k+1 |
∴当n=k+1时,命题成立.…(11分)
由(1)(2)知,对一切n,(n≥2,n∈N*)有g(n)=n,使得a1+a2+a3+…+an-1=g(n)(an-1)都成立.…(12分)
点评:本题考查数列递推关系式及数学归纳法,着重考查推理与论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若点P(-1,2)在角θ的终边上,则tanθ等于( )
| A、-2 | ||||
B、-
| ||||
C、-
| ||||
D、
|
定义区间(a,b)、[a,b)、(a,b]、[a,b]的长度d均为d=b-a,多个互无交集的区间的并集长度为各区间长度之和,例如(1,2)∪[3,5)的长度d=(2-1)+(5-3)=3.用[x]表示不超过x的最大整数,例如[2]=2,[3.7]=3,[-1.2]=-2.记{x}=x-[x],设f(x)=[x]•{x},g(x)=x-1,若用d1、d2和d3分别表示不等式f(x)>g(x)、方程f(x)=g(x)和不等式f(x)<g(x)解集区间的长度,则当0≤x≤2013时,有( )
| A、d1=1,d2=2,d3=2010 |
| B、d1=1,d2=1,d3=2011 |
| C、d1=3,d2=5,d3=2005 |
| D、d1=2,d2=3,d3=2008 |
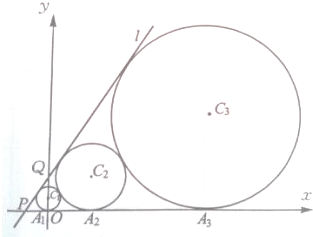 如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,
如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,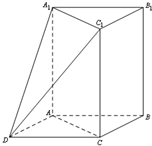 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.