题目内容
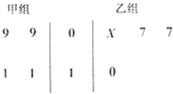 如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.(1)求甲组同学植树的方差;
(2)乙组同学植树的方差会不会小于甲组同学植树的方差?请说明理由.
考点:极差、方差与标准差,茎叶图
专题:概率与统计
分析:(1)先求出甲组同学植树的平均数,再求甲组同学植树的方差.
(2)由已知得S乙2=3(t-2)2+
,当t=2时,即x=8时,S乙2取得最小值
>1=S甲2,从而乙组同学植树的方差不会小于甲组同学植树的方差.
(2)由已知得S乙2=3(t-2)2+
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)
=
(9+9+11+11)=10,
S甲2=
[(9-10)2+(9-10)2+(11-10)2+(11-10)2]=1.
(2)
=
(x+7+7+10)=
+6,令
=t,则
=t+6,
则S乙2=
[(3t-6)2+(7-t-6)2+(7-t-6)2+(10-t-6)2]=3(t-2)2+
,
当t=2时,即x=8时,
S乙2取得最小值
>1=S甲2,
∴乙组同学植树的方差不会小于甲组同学植树的方差.
. |
| x甲 |
| 1 |
| 4 |
S甲2=
| 1 |
| 4 |
(2)
. |
| x乙 |
| 1 |
| 4 |
| x |
| 4 |
| x |
| 4 |
. |
| x乙 |
则S乙2=
| 1 |
| 4 |
| 3 |
| 2 |
当t=2时,即x=8时,
S乙2取得最小值
| 3 |
| 2 |
∴乙组同学植树的方差不会小于甲组同学植树的方差.
点评:本题考查方差的求法及应用,是基础题,解题时要注意方差计算公式的合理运用.

练习册系列答案
相关题目
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程x3+x2-2x-2=0的一个近似根(精确度为0.05)为( )
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
| A、1.275 | B、1.375 |
| C、1.415 | D、1.5 |
方程x2+ky2=1表示焦点在y轴上的椭圆,则k的范围( )
| A、(0,+∞) |
| B、(0,2) |
| C、(0,1) |
| D、(1,+∞) |
已知实数x,y满足
,则(x+1)2+(y-1)2的最小值是( )
|
| A、2 | ||
| B、5 | ||
C、
| ||
D、
|