题目内容
已知函数f(x)=2
sinxcosx-(sinx+cosx)(sinx-cosx).
(1)若f(x)=1,求x的值;
(2)求函数y=f(x)的单调增区间;
(3)若x∈[0,
],求函数y=f(x)的值域.
| 3 |
(1)若f(x)=1,求x的值;
(2)求函数y=f(x)的单调增区间;
(3)若x∈[0,
| π |
| 2 |
考点:两角和与差的正弦函数,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(1)利用三角恒等变换可得f(x)=2sin(2x+
),由f(x)=1,利用正弦函数的性质可求x的值;
(2)利用正弦函数的单调性,由不等式2kπ-
≤2x+
≤2kπ+
(k∈Z),即可求得函数y=f(x)的单调增区间;
(3)x∈[0,
]⇒2x+
∈[
,
],利用正弦函数的图象与性质即可求得该区间上函数y=f(x)的值域.
| π |
| 6 |
(2)利用正弦函数的单调性,由不等式2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(3)x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:(1)∵f(x)=2
sinxcosx-(sinx+cosx)(sinx-cosx)=
sin2x+cos2x=2sin(2x+
)=1,
∴sin(2x+
)=
,
∴2x+
=2kπ+
或2x+
=2kπ+
(k∈Z),
∴x=kπ或x=kπ+
(k∈Z).
(2)由2kπ-
≤2x+
≤2kπ+
(k∈Z),得:kπ-
≤x≤kπ+
(k∈Z).
∴函数y=f(x)的单调增区间为[kπ-
,kπ+
](k∈Z);
(3)∵x∈[0,
],∴2x+
∈[
,
],
∴sin(2x+
)∈[-
,1],
∴函数y=f(x)的值域为[-1,2].
| 3 |
| 3 |
| π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴x=kπ或x=kπ+
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数y=f(x)的单调增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(3)∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴函数y=f(x)的值域为[-1,2].
点评:本题考查两角和与差的正弦函数,着重考查正弦函数的单调性与闭区间上的值域,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
集合A={x|x≥1},B={x|-1<x<2},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|x>-1} |
| C、{x|1≤x<2} |
| D、{x|-1<x<2} |
下列函数中是偶函数且在(0,1)上单调递减的是( )
A、y=-x
| ||
| B、y=x4 | ||
C、y=x
| ||
| D、y=x-2 |
若a=20.5,b=log20.5,c=log21.5,则( )
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、b>c>a |
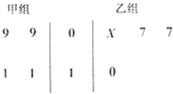 如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.