题目内容
已知实数x，y满足
，则（x+1）2+（y-1）2的最小值是（ ）
|
| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．
解答：
解：设z=（x+1）2+（y-1）2，则z的几何意义为点（x，y）得定点D（-1，1）的距离的平方，
出不等式组对应的平面区域如图：
由图象可知BD的距离最大，
点D到直线2x+y-2=0的距离最小，
此时d=
=
，
则z=d2=
，
故选：D
出不等式组对应的平面区域如图：
由图象可知BD的距离最大，
点D到直线2x+y-2=0的距离最小，
此时d=
| |-2+1-2| | ||
|
| 3 | ||
|
则z=d2=
| 9 |
| 5 |
故选：D
点评：本题主要考查线性规划的应用，利用z的几何意义以及点到直线的距离公式是解决本题的关键，注意使用数形结合．
练习册系列答案
相关题目
斜边长为2的直角三角形的面积的最大值为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
如图，在△ABC中，M是AC的中点，点E在AB上，且AE=| 1 |
| 4 |
| A、2：1 | B、3：1 |
| C、3：2 | D、4：1 |
下列函数中是偶函数且在（0，1）上单调递减的是（ ）
A、y=-x
| ||
| B、y=x4 | ||
C、y=x
| ||
| D、y=x-2 |
已知圆的圆心是（-3，4），半径长是
，则圆的标准方程为（ ）
| 5 |
| A、（x+3）2+（y-4）2=5 |
| B、（x-3）2+（y-4）2=5 |
| C、（x+3）2+（y-4）2=25 |
| D、（x+3）2+（y+4）2=25 |
若a=20.5，b=log20.5，c=log21.5，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、b＞c＞a |
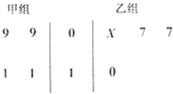如图茎叶图记录了甲、乙两个组四名同学的植树棵树．乙组记录中有一个数计模糊，无法确认，在图中以X表示．
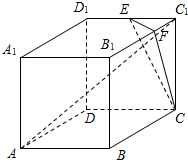如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，∠DAB=45°，AA1=AB=2，AD=2