题目内容

求关于x的方程7x2-（k+13）x+k2-k-2=0满足0＜x1＜1＜x2＜2的两个实数根的充要条件．
考点：必要条件、充分条件与充要条件的判断
专题：函数的性质及应用,简易逻辑
分析：设f（x）=7x2-（k+13）x+k2-k-2，利用二次函数根的分布，建立条件关系即可得到结论．
解答： 解：设f（x）=7x2-（k+13）x+k2-k-2，
∵0＜x1＜1＜x2＜2，
∴
f(0)=k2-k-2＞0
f(1)=k2-2k-8＜0
f(2)=k2-3k＞0
，
则
k＞2或k＜-1
k＞4或k＜-2
k＞3或k＜0
，
即k＞4或k＜-2，
则方程7x2-（k+13）x+k2-k-2=0满足0＜x1＜1＜x2＜2的两个实数根的充要条件是k＞4或k＜-2．
点评：本题主要考查函数与方程之间的关系，构造函数，转化为二次函数根的分布是解决本题的关键．
练习册系列答案
相关题目
设不等式组
6x-y≥8
2x-3y≤0
2x+y≤8
表示的平面区域为r，且函数y=logax的图象经过区域r，则实数a的取值范围是（　　）
A、（1，
3
]
B、[
42
，
3
2
]
C、[
42
，
3
]
D、[
3
2
，
3
]
已知变量x、y满足条件
x≥1
x-y≤0
x+2y-9≤0
，则2x+y的最大值是（　　）
A、3B、6C、9D、12
已知直线l的参数方程为
x=-10+t
y=t
 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ2-4ρsinθ+2=0．
（Ⅰ）把圆C的极坐标方程化为直角坐标方程；
（Ⅱ）将直线l向右平移h个单位，所得直线l′与圆C相切，求h．
曲线x2+y2=2与曲线y=x2所围成的区域的面积是多少？
在△ABC中．∠BAC=120°，AB=3，BC=7．
（1）求AC的长；
（2）求△ABC的面积．
在△ABC中，角A，B，C所对的边长分别为a，b，c，若△ABC的周长为
2
+1，且sinA+sinC=
2
sinB．
（1）求边长b；
（2）若△ABC的面积为
1
6
sinB，求角B的度数．
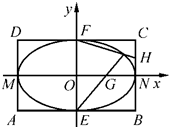如图，矩形ABCD中，|AB|=4，|BC|=2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．
（Ⅰ）证明：直线EG与FH的交点L在椭圆Ω：
x2
4
+y2=1上；
（Ⅱ）设直线l：y=x+m（-1≤m≤1）与椭圆Ω：
x2
4
+y2=1有两个不同的交点P，Q，直线l与矩形ABCD有两个不同的交点S，T，求
|PQ|
|ST|
的最大值及取得最大值时m的值．
求证：（1）a2+b2+c2≥ab+ac+bc；  
（2）
6
+
7
＞2
2
+
5
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网