题目内容
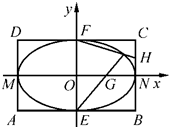 如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.(Ⅰ)证明:直线EG与FH的交点L在椭圆Ω:
| x2 |
| 4 |
(Ⅱ)设直线l:y=x+m(-1≤m≤1)与椭圆Ω:
| x2 |
| 4 |
| |PQ| |
| |ST| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件求出直线EG:y=x-1,直线FH:y=-
x+1,从而得到直线EG与FH的交点,由此能证明直线EG与FH的交点L在椭圆Ω上.
(Ⅱ)联立
,得5x2+8mx+4m2-4=0,由△=64m2-20(4m2-4)>0,且-1≤m≤1,得-1≤m≤1,由此能求出
的最大值.
| 1 |
| 4 |
(Ⅱ)联立
|
| |PQ| |
| |ST| |
解答:
(Ⅰ)证明:∵矩形ABCD中,|AB|=4,|BC|=2,
E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点,
∴点E(0,-1),G(1,0),F(0,1),H(2,
),(1分)
∴直线EG:y=x-1,直线FH:y=-
x+1,(3分)
∴直线EG与FH的交点L(
,
),(4分)
∵
+(
)2=1,
∴直线EG与FH的交点L在椭圆Ω:
+y2=1上.(5分)
(Ⅱ)解:联立方程组
,
消去y,得5x2+8mx+4m2-4=0,(6分)
设P(x1,y1),Q(x2,y2),
则x1+x2=-
,x1x2=
,(7分)
由△=64m2-20(4m2-4)>0,且-1≤m≤1,
得-1≤m≤1.(8分)|PQ|=
=
•
=
,(10分)
由于-1≤m≤1时,直线l与矩形ABCD的边AB、CD相交,
∴|ST|=2
,(11分)
则
=
,
∴m=0时,
取最大值
.(13分)
E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点,
∴点E(0,-1),G(1,0),F(0,1),H(2,
| 1 |
| 2 |
∴直线EG:y=x-1,直线FH:y=-
| 1 |
| 4 |
∴直线EG与FH的交点L(
| 8 |
| 5 |
| 3 |
| 5 |
∵
(
| ||
| 4 |
| 3 |
| 5 |
∴直线EG与FH的交点L在椭圆Ω:
| x2 |
| 4 |
(Ⅱ)解:联立方程组
|
消去y,得5x2+8mx+4m2-4=0,(6分)
设P(x1,y1),Q(x2,y2),
则x1+x2=-
| 8m |
| 5 |
| 4m2-4 |
| 5 |
由△=64m2-20(4m2-4)>0,且-1≤m≤1,
得-1≤m≤1.(8分)|PQ|=
| (1+k2)[(x1+x2)2-4x1x2] |
| 2 |
(-
|
4
| ||
| 5 |
| 5-m2 |
由于-1≤m≤1时,直线l与矩形ABCD的边AB、CD相交,
∴|ST|=2
| 2 |
则
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5-m2 |
∴m=0时,
| |PQ| |
| |ST| |
2
| ||
| 5 |
点评:本题考查两直线的交点在椭圆上的证明,考查两线段比值的最大值的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知空间图形的三视图如图,空间几何体的表面积为( )
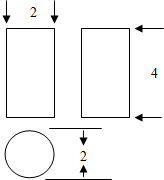

| A、8π | B、10π |
| C、12π | D、9π |
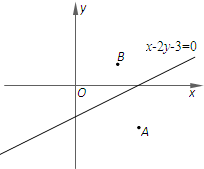 已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.
已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.